Why are fractions so difficult for students?

Foto por Steve Hodgson; licensiado por CC BY-SA 2.0

Fractions and fraction math in middle school is notoriously difficult. But why is it that so many students seem to have trouble with them? Let's take a look at some factors that enter the situation.

Concept of a fraction

First of all, the concept of a fraction comes from DIVISION: for example, 4/5 is the answer to the division 4 ÷ 5.

Conceptually, we can think of, say, four apples that are divided evenly among five people: each person gets 4/5 of an apple. Or, 1/3 is the result if you divide ONE cucumber between THREE people: each person gets 1/3 of the cucumber.

However, we also use fractions in the context of sets of objects. If Steven has 24 toy cars, then 1/3 of them is eight cars.

These two types of usages can be confusing. In each case, we have a "whole" and a part: either the "whole" is ONE of something (one cucumber), or the "whole" is an entire set, and then we look at a part of that "whole".

Students need practice differentiating between these two types of part/whole relationships.

But the MAIN way fraction math becomes challenging is in learning the various operations with fractions.

Operations with fractions

What makes it difficult is that there are MANY "operations" (ways to manipulate fractions), and the rules for these use the common operations with whole numbers in a myriad of different ways.

Just look at the amount of operations there are to learn about fractions — and the rules for those!

If students don't understand where these rules come from, they can seem like a meaningless jungle, like "magic", where you do various random things with the numerators and denominators to come up with the answer.

Students can then become blind followers of the rules, spitting out the answers but not having any idea if the answers are reasonable or not. Besides, it is easy to forget these rules after a few years of not using them.

The solution: use visual models A LOT

To help children master fractions, I like to use visual models or manipulatives in a more extensive manner than most curricula do. In Math Mammoth materials, students solve lots of problems with visual models or fraction manipulatives.

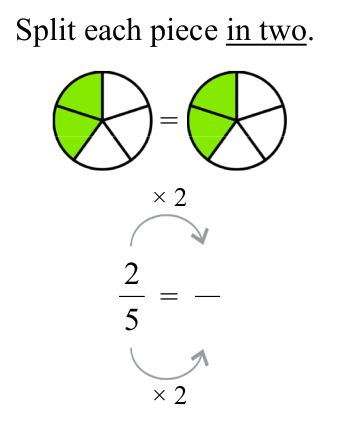For example, here you see a VISUAL method for equivalent fractions: each piece is split further into a certain number of new pieces.

Working with visual models helps students form these same pictures in their minds, and they can then actually THINK through the fraction pictures, to do certain fraction operations.

Another example — student multiplies a fraction by a whole number. The answer is found via the visual model, not by using a rule. (Later, the rule is introduced — but the student has probably discovered it on their own by that point.)

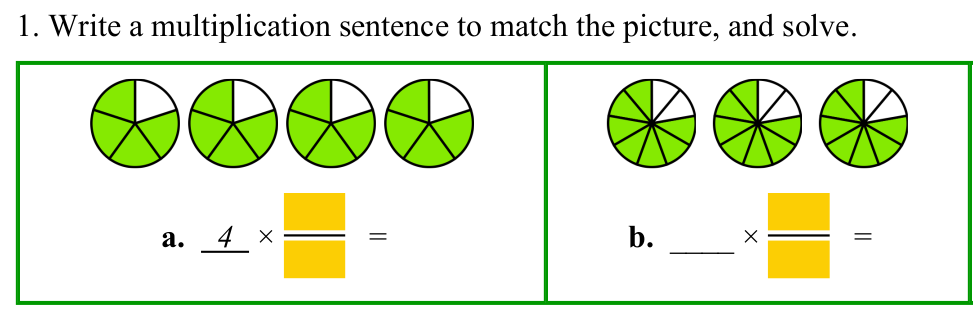
When students get lots of 'hands-on' experiences with fraction pictures (many of which they draw themselves), they may even find the rule THEMSELVES — and it will make sense.

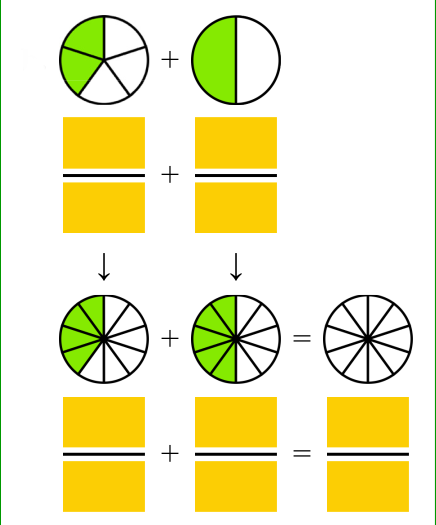Another example is the topic of adding unlike fractions. The teacher can show how the pieces in the fractions need to be split further so that they are all the SAME KIND of pieces (common denominator) — and then we can add.

I'm not saying that the rules are not needed — because they are. You cannot get through algebra without knowing the actual rules for fraction operations. But by using visual models extensively in the beginning stages, the rules will make more sense, and if 10 years later you have forgotten the rules, you should still able to "do the math" with the pictures in you mind, and not consider fractions as something you just "cannot do".

Help with fractions

These worktexts explain fraction operations using a visual model of a pie, and let the students practice sufficiently with visual exercises so they will understand the concepts. They suit best 4th-5th grades but can be used in later grades also:

Math Mammoth Introduction to Fractions

A self-teaching worktext for grades 3-4 that covers fractions, mixed numbers, comparing fractions, equivalent fractions, adding and subtracting like fractions, and multiplying a fraction by a whole number.

Math Mammoth Fractions 1

A self-teaching worktext that covers mixed numbers, equivalent fractions, adding and subtracting like & unlike fractions, adding and subtracting mixed numbers, comparing fractions, and finding a fractional part of a group.

Math Mammoth Fractions 2

A self-teaching worktext, sequel to Math Mammoth Fractions 1. Covers simplifying fractions, multiplying fractions and mixed numbers, and dividing fractions and mixed numbers.

I also sell a fractions worktext for grade 6, Fractions & Decimals 3.

Secondly, check out my free videos for fraction operations: