This is a great set of interactive activities for students in 8th grade or in algebra 1, allowing them to practice the slope-intercept form of the equation of a line in detail.
It has three different activities or illustrations, and a game.
1. "Slope" is an illustration of the concept of slope, showing two points in a coordinate grid, and the calculation for slope. You can drag the points, and see how the calculation and the rise and the run change -- OR, you can change the numbers in the calculation and see the line change.
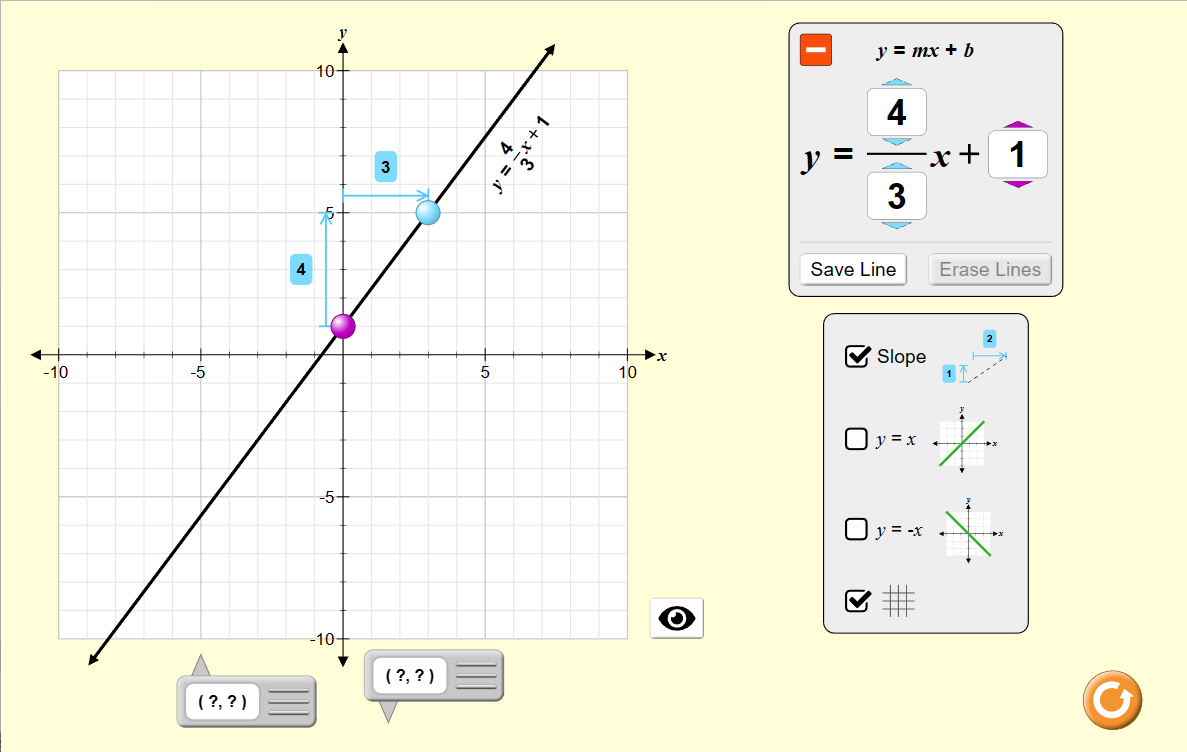
2. "Slope-Intercept". In this activity, you can move the two points (dots) that define a line, and see the rise, the run, the slope, and the equation of the line, and how those change as you drag the dots.
Alternatively, you can change the slope (the rise/run) and the y-intercept of the equation, and see the line and the dots change in the coordinate grid.
This activity works great as an illustration of the slope-intercept form of the equation of the line. A teacher can use it to explain these concepts to students, and to ask them questions in class, or students can use this to explore and practice these concepts.
3. Point-Slope activity operates with the point-slope form of the equation for a line: y − y1 = m(x − x1). The purple point is the "point" (x1, y1) used in the equation, and the blue point is another point on the line that then determines the slope. You can move either point, or you can set the numbers in the equation and see the line and the points move.
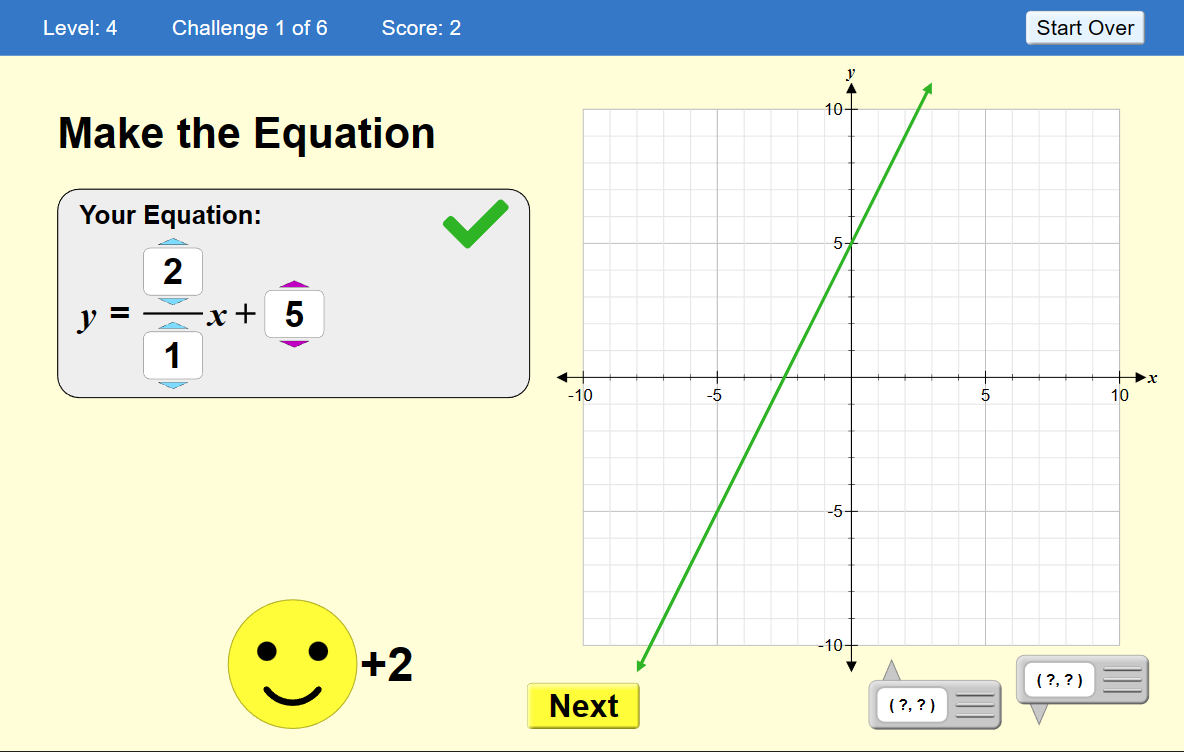
4. Line Game. Practice plotting lines when an equation in slope-intercept form is given, or telling the slope and y-intercept when a graph is given.
You are either given an equation of a line to graph, and you need to set the slope or the y-intercept of the line in the coordinate grid by dragging a point. Or, you are given a line in the coordinate grid, and asked the slope or the y-intercept.
The game six four levels of difficulty, and includes vertical, horizontal, increasing, and decreasing (negative slope) lines.
Credit: This activity is created by PhET
Screenshots from the game and activity: