Maria's Math Tips, February 2016
Hello again! smile
  1. Math Mammoth news
  2. Telling time (grades 2-3)
  3. Note on mental math (grades 1-6)
  4. Puzzles from Nrich (grades 1-12)
  5. Videos for the multiplication tables (grades 2-4)

1. Math Mammoth news

If you didn't yet hear about this, I'll mention it again:

We now have Math Mammoth International Version available!

cover for Math Mammoth Grade 1-B Complete Worktext Currently available for grades 1-6, this version differs from the US version in these aspects:
  • The currency used in the money chapters in grades 1-3 is the Australian dollar. (The download versions for these grades include the chapter on money also for US, British, European, South African, Canadian, and New Zealand currencies.)
  • The curriculum teaches the metric measurement units. US customary units, such as inches and pounds, are not used.
  • The spelling conforms to British international standards (British English).
  • Page (paper) size is A4.
  • Large numbers are formatted with a space as the thousands separator (such as 12 394). (The decimals are formatted with a decimal point, like in the US version.)
Check it out at the link below:
Math Mammoth, International version

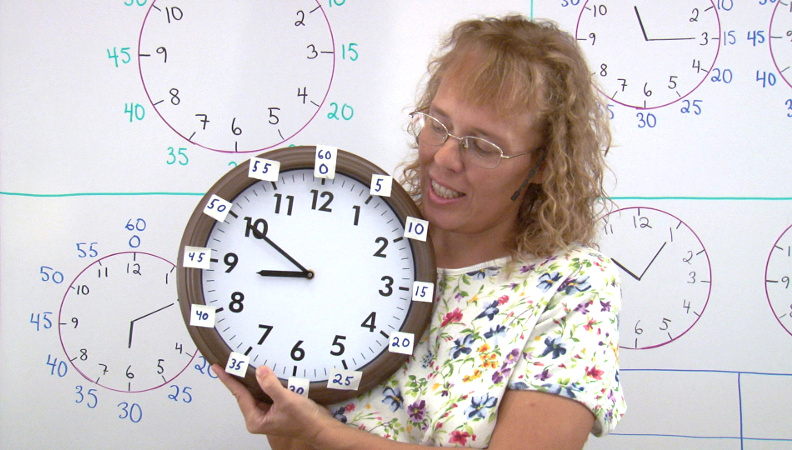
2. Telling time

Check out these videos of mine on telling time, meant mostly for grades 2-3, but I will be adding some for 1st grade hopefully soon.

Tell time to the nearest five minutes - grades 2-3

Elapsed time - whole hours - grades 1-3

Tell time using "past" and "till" - grades 2-3

3. Note on mental math

Someone stated this to me recently concerning her son...
"Also I don't feel he is proficient in mental math addition and subtraction of large numbers either. Ex: 3125+6261. I don't know if it's because of me or not enough teaching material to show him or not enough practice for him."

I answered the person this way:

just wanted to drop a short note that I personally would not expect students to do 4-digit addition mentally; I myself don't do that. One characteristics of efficient problem-solvers is that they decide which TOOL is the best & most efficient to use for each calculation.

The tools are: your mind, calculator, and paper & pencil.

I have included a lot of simple mental math in my books, because your mind clearly is faster for solving 10 x 56 or 25 + 26 than reaching for a calculator, punching in the numbers, and getting the result. But at some point... maybe with 3 or 4-digit additions, the calculator becomes faster. So, I feel students need to know HOW to do such additions on paper and pencil, and HOW to do 3-digit additions even mentally, but when it comes to actual real-life situations, mental addition is not always the best choice... it DEPENDS on the numbers involved, and many other factors.

Students DO need to learn mental math also for this reason: it builds "number sense", which then helps them understand algebra. But there's a limit... there's no need to go "overboard" with it, either.

See also my article on number talks — short math problems where we let everyone voice how they came up with the answer (using mental math).

4. Puzzles from Nrich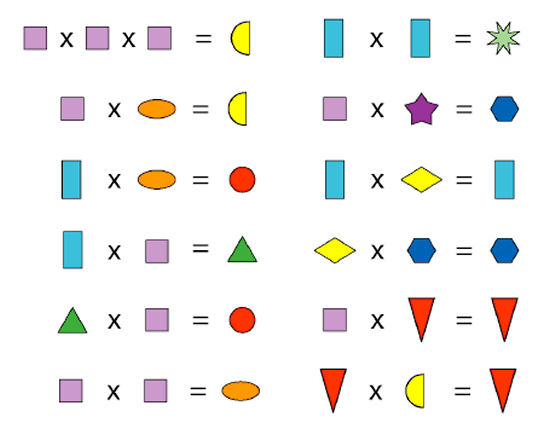

I found a neat "algebraic" multiplication puzzle for elementary school children...

Shape Times Shape Puzzle

These eleven shapes each stand for a different number. Can you work out what they are?

From NRICH - home of "rich" mathematics smile

Here's another one from the same site... a true mathematical exploration!

Consecutive Numbers

My 7th grader enjoyed this math activity a lot (I called it an "exploration" for her). We did it together, as I didn't know the "right answer" or how it would go.

You choose four consecutive numbers, such as 7, 8, 9 and 10. Then you place + and − signs in between to make an expression, such as

7 + 8 − 9 + 10

Try all different combinations of + and - signs, and see what ANSWERS you get.

Then change your numbers. And try a third set of numbers also. You'll notice something interesting!

I even made a simple spreadsheet to work it out in a spreadsheet program.

In the end, I showed my daughter how to present four consecutive numbers ALGEBRAICALLY... we will have

n, n + 1, n + 2, and n + 3.

Then, she actually figured out the algebraic expressions for all the possibilities of + and - signs between them. For example, one of them would be

n + (n + 1) − (n + 2) − (n + 3)

It ended up being a NEAT demonstration of the power of algebra: the POWER of GENERALIZATION. She was able to see the results of the exploration in a GENERAL sense, instead of simply trying different individual numbers.

Nrich.maths.org has lots more to offer — puzzles, games, and explorations. Check it out!

5. Videos for the multiplication tables

I know I included this already in my previous newsletter, but I'm including it again, because I feel it is important enough to mention twice :).

I've made a series of videos to help students/children learn the multiplication tables from 2 to 12. They are presented in a specific order — easiest ones first — which makes learning them MUCH easier.



Each teaching video has a similar structure:
  1. First, we study the SKIP-COUNTING list or pattern for the specific table.
  2. Next, I drill the table itself, but the STRUCTURE of the table is visible to the student during the drill. This ties the table with the just-learned skip-counting list, and also helps the student to use the CONCEPT of multiplication to possibly figure out some of the answers that are not yet memorized.
  3. Lastly, we practice the table backwards. For example, I ask, "How many times 5 is 35?" This essentially teaches the basic division facts at the same time (though, I don't mention them as such).


The series of videos also include "INTERLUDES": short video lessons in which we look at multiplication patterns, missing factors, word problems, and puzzles.

Check out also my article on how to learn the multiplication tables.

And don't miss Mathy's (my mascot) VICTORY DANCE after having studied all the times tables: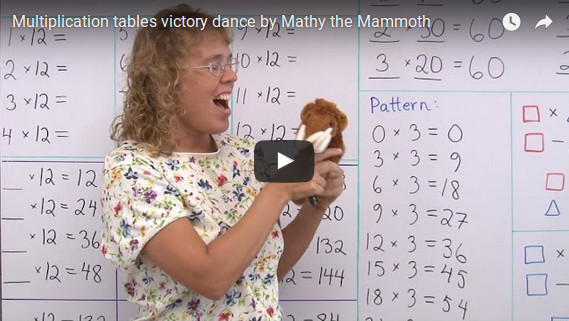




Thanks for reading! :)

Feel free to forward this issue to a friend/colleague! Subscribe here.

Till next time,
Maria Miller
Topical worktexts Complete curriculum Placement tests
 
Math Mammoth freebies Math Mammoth on Facebook Newsletter Archives








--