Maria's Math News, November 2021

Hi again!

I hope you enjoy this month's collection of tips. 😀

Math Mammoth news
Delaying formal arithmetic
Multiplication Tic Tac Toe (grades 3-5)
Visualizing probabilities (grades 7-12)
Something kind of cool!
Just for fun!

1. Math Mammoth news

Math Mammoth sale! Starting now, through December 3, get ALL Math Mammoth downloads & CDs at 25% off!

Start browsing the books here:

Start shopping >

Another testimonial in...

Dear Mrs. Miller: thank you so very much for your math program, and also for your recommendation of Math Without Borders for high school math. We found your program to be exactly what we needed at the right time. After finding CTC Math to be a bad fit for us, my kiddo wanted a workbook, and your program was wonderful. We especially liked the balance problems as an introduction to the concept of Algebra.

Mr. Chandler's Math Without Borders has also been a very good fit for us. We chose him over flashier programs because he had "real information" in his lessons (my kiddo's opinion). I simply wanted to let you know how your program and your advice have been received by this family.

Thank you,
- Sarah Kline

2. Delaying formal arithmetic

Back a few years ago, Denise at Let's Play Math discussed delaying formal arithmetic, as based on Benezet's experiment in the early 1900s.

I have read the whole story (The Teaching of Arithmetic I: The Story of an Experiment) and it's a FASCINATING, though a long read! These kids ended up having superior math skills in middle school.

Anyhow, Denise has highlighted some points of this "experiment" and you might enjoy her posts.

This article covers it also.

Personally, I do like to introduce "formal" or paper-pencil arithmetic earlier than Benezet did... as is customary in today's culture, BUT it's beneficial to be aware of how things can work without it also! You might get some ideas to use in your own teaching.

3. Multiplication Tic Tac Toe

Another multiplication game... I really like this one! Very simple too. You will need a multiplication tables chart (empty) and two colors (for two players).

Read the directions here: Multiplication Tic Tac Toe.

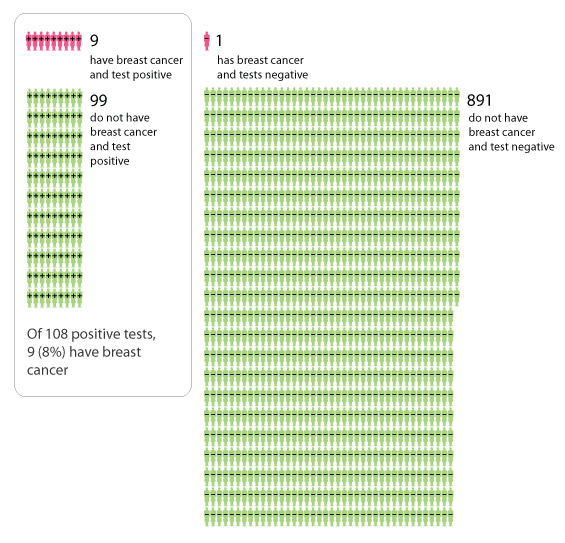
4. Visualizing probabilities

This is a wonderful article about modern visualization techniques in the context of probabilities. The right picture really can be worth a thousand words.

As an example, the author looks at the probability that a woman who tests positive for breast cancer actually has breast cancer. This probability is not 100%!

In other words, if the test says you're positive, it's not a sure thing you actually are! That's because tests are not 100% accurate.

"To pin this question down, let us consider a population in which 1% of women have breast cancer, and a mammography test which has a 90% chance of returning a correct result. That is, if a woman has cancer then there is a 90% chance the test will be positive, and if a woman does not have cancer then there is a 90% chance the test will be negative. Suppose a particular woman tests positive; what is the probability that she has breast cancer? The answer may seem surprising."

5. Something kind of cool!

When you divide 1 by 998,001, the resulting decimal starts like this:

0.000001002003004005006007008009010011012013014015016017
018019020021022023024025026027028029030031032...

It's a recurring (repeating) decimal, and its decimal expansion actually has ALMOST ALL three-digit numbers from 1 through 999! It only misses 998.

Now, 998,001 happens to be the square of 99. A similar thing happens if you divide 1 by the square of 9... 1 divided by 81. We get:

0.012345679012345679012345679...

The decimal expansion has all one-digit numbers from 0 through 9, except 8.
Kind of cool, right?
Hat tip to Brilliant Learning.

6. Just for fun!

Thanks for reading! 🙂

Feel free to forward this issue to a friend/colleague! Subscribe here.

Till next time,
Maria Miller