Hello again!
|
1. Math Mammoth NewsWe're still getting ready with new 2020 editions for grades 4 and 5 (in the Light Blue series complete curriculum). The new editions for grade 4 and grade 5 are already available for purchase at the site — there's an "Add to cart" button for them in the sidebar of the product page. However, the samples, lesson plans, and some other info is not yet updated everywhere.Read about the changes in grade 4, and in grade 5. If have purchased the digital version in the past, and you need the new edition, you can now get the update. Send an email to  , and include your email receipt from the past, if possible. If not, then give all the information you can about your purchase: which store, the name/email used, approximate date, etc.
However, I am hoping that some of you are not in a hurry and can wait a week or two; it will make life easier as we might get quite a few requests! Coming soon... the traditional thanksgiving SALE! Stay tuned! |
2. Why are fractions so difficult for many students? It's often not so much the concept of a fraction that is difficult — it is the various OPERATIONS with fractions: addition, subtraction, multiplication, division, comparing, simplifying, etc. Just look at the amount of rules there are to learn about fractions!
There are SO many rules to learn when it comes to fraction arithmetic! If students don't understand the concepts, all or most of these rules will likely be forgotten after a while What can we do? Continue reading... |
3. SPIRAL multiplication game We made the game board bigger by using a double deck, and after one round, we changed to using TWO dice instead of one, and adding those to get the multiplier. That way you will get bigger numbers more often — and you will travel quicker through the board also.😄 |
4. Understanding the concept of divisionHere's an old post from my 2009 newsletter... 😃Finnish researchers gave this division problem to high school students and pre-service teachers: We know that: I really like the question. To solve it, you need to TRULY understand what DIVISION and remainders are all about! Now, let's think about it. Have you ever seen a pattern in division and remainders, like the one below? 20 ÷ 4 = 5 Students need to see and do such patterns when they are first learning basic division. The pattern shows that every fourth number is evenly divisible by 4, and the ones in between have remainders 1, 2, or 3 in order. If the answer is given as a mixed number, the remainder is the numerator. Using a similar pattern will solve the original question fairly easily.😁 Give it a try! Or see the full answer here. |
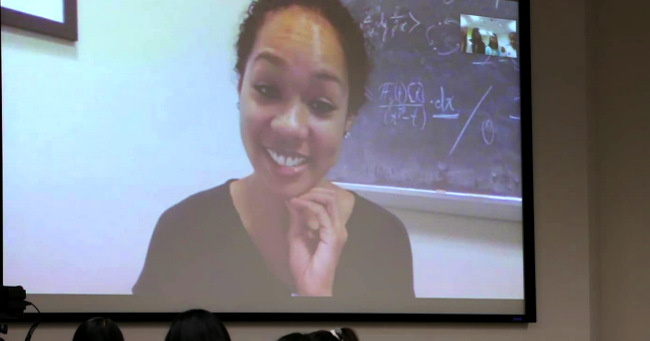
5. Inspirational! A short inspirational video from a young mathematician whose life and career trajectory was completely changed by just one teacher influencing her to THINK DIFFERENTLY about mathematics, during one of her college math classes. Math isn't just about memorizing formulas! I personally also learned to LOVE mathematics after high school... in university... when the focus of the instruction changed more towards proof, structure, and logic... all of that somehow really fascinated me. |
6. Digit disguises |
7. Just for fun!Thanks for reading!  Feel free to forward this issue to a friend/colleague! Subscribe here. Till next time, Maria Miller 
|
| Privacy & your personal data | Contact | Math Mammoth freebies | Placement tests |
| Complete curriculum | Why was the fig tree cursed? | Visit us on Facebook | Newsletter Archives |