Math Mammoth and the Common Core Standards

Many parents and teachers are very worried about the Common Core Standards, and some are actively fighting against it. There is a lot of confusion, anger, uncertainty—and even some misinformation. In this document, it is my hope to clarify my position and thinking concerning the Common Core Standards (CCS).

Math Mammoth's position
Thoughts about testing
Common Core and common sense
Bad examples of "common core" or "new math"
Conceptual math
Details of the alignment (a separate page)

Do I support the CCS?

This is my "position" in a nutshell:

• To me, standards are just standards: statements that dictate what students should learn on a particular grade level. I am not "for" them nor "against" them. I have never considered them in a political way, and in fact, I do want to stay out of politics. I feel sad if the CCS are used as a means to achieve political goals.
• As statements that dictate what students should learn and when, I feel the CCS are an improvement over most states' previous standards — but I also feel that they are not perfect.
• My decision to align Math Mammoth Light Blue Series in 2011 to the CCS was based solely on these facts: 1) The standards themselves are reasonable. 2) At the time (2011), practically all the states had decided to adopt them.
  
  Even now, after seeing all the turmoil over them, I still feel that Math Mammoth, being aligned, can help many homeschoolers (those who use charter schools, for example). And, the alignment has not made Math Mammoth materials any worse, so those who don't have to worry about the standards are not hurt by using MM.
• The math standards are more rigorous than what states are used to, and thus it comes as no surprise to me that schools have a lot of problems implementing the standards. After seeing some examples of supposedly "common core" or "new math" problems, I am SURE that some people producing math materials do not even understand the standards properly! I feel all of this is quite unfortunate and saddening.
• If I had my say in the whole public school system of the United States, I would reduce testing tremendously and write a set of national non-binding guidelines/standards that would be fewer in number and less restricting than the CCS.

Thoughts about testing

Overall, I think the US is doing far too much testing of students on every level (local and national). Testing can be harmful... read my article about timed tests and how they can damages students' learning of math.

I do not support all of this testing going on, no matter what standards it is based on, but unfortunately it's not up to me whether our students will be tested. Even some homeschooled students will be required to take math tests based on their state standards, which in many cases will be the CCS. As of this writing (March 2014), it is still to be seen how the tests based on the CCS will look like.

Common Core and Common Sense

What follows is my take on some math problems of supposedly "common core math" or "new math" that have circulated on the internet. I feel they show us a misdirected implementation of the CCS.

Keep in mind, not everything you see in math books or on the internet is properly done based on the CCS. In some of the examples you see, it looks like people are throwing out common sense when making math problems to address the common core standards!

I am not surprised that the implementation has ended up "botched" in some places. The CCS are such a change to most teachers that they need lots of support and re-education before they are required to teach to them.

I have always thought that the MAIN problem facing math education in elementary grades in public schools is that many elementary teachers do not understand mathematics sufficiently to be able to teach it right even in elementary level. For example, many of them do not understand the concepts, the why's and wherefores of the algorithms they teach. It's not their fault - the problem traces back to what they were taught in teacher training and in their own schooling.

Even the standards document itself is somewhat hard to follow in places. Reading it requires some thinking. I wish someone would produce a booklet that explains the standards in simple language and with numerous examples. (Update: Someone has! Check out The Common Core Mathematics Companion: The Standards Decoded series of books.)

Bad examples of "common core" or "new math"

Example 1

Recently I saw an image of subtraction strategies on Facebook that claimed it was from a 1st grade math book and was "Common Core math."

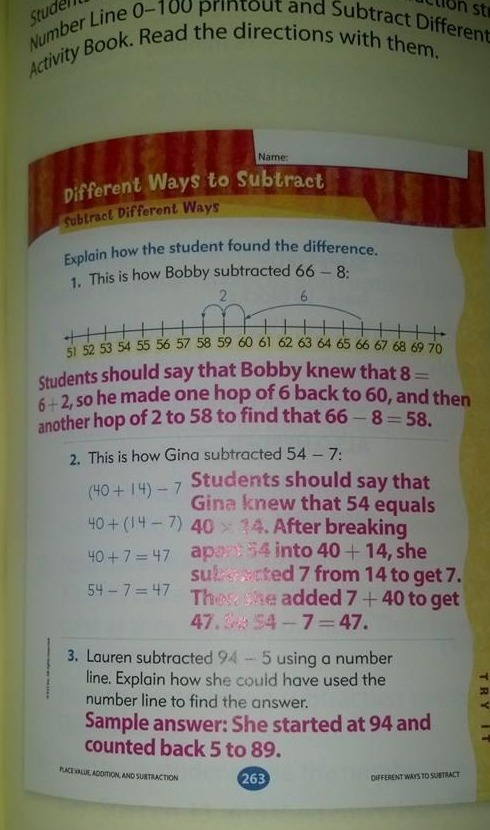
I think method 2 is way too difficult for 1st grade, and I'd leave even method 1 for 2nd grade.

However, that book doesn't seem to even align with the Common Core standards. The standards for 1st grade simply don't include those kinds of subtraction problems!

This is what we find in the standards:

Add and subtract within 20.
1.OA.5
Relate counting to addition and subtraction (e.g., by counting on 2 to add 2).

1.OA.6.
Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decomposing a number leading to a ten (e.g., 13 − 4 = 13 − 3 − 1 = 10 − 1 = 9); using the relationship between addition and subtraction (e.g., knowing that 8 + 4 = 12, one knows 12 − 8 = 4); and creating equivalent but easier or known sums (e.g., adding 6 + 7 by creating the known equivalent 6 + 6 + 1 = 12 + 1 = 13).

The textbook example seems to want to address 1.OA.6 above, but that is clearly for adding and subtracting within 20, not with larger numbers.

Later in the 1st grade standards we see two standards that have to do with subtracting two-digit numbers (within 100):

1.NBT.5.
Given a two-digit number, mentally find 10 more or 10 less than the number, without having to count; explain the reasoning used.

1.NBT.6.
Subtract multiples of 10 in the range 10-90 from multiples of 10 in the range 10-90 (positive or zero differences), using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.

Maria's note: this means subtractions such as 34 — 20 or 89 — 60.

but neither of these includes subtractions such as 54 − 7 or 82 − 6. Those are in 2nd grade:

2.NBT.5
Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.

Note that the 2nd grade standard does not specify HOW you subtract (whether you use mental math strategies or write numbers under each other and borrow/regroup).

Example 2

From Houghton Mifflin, supposedly:

Juanita wants to give bags of stickers to her friends. She wants to give the same number of stickers to each friend. She's not sure if she needs 4 bags or 6 bags of stickers. How many stickers could she buy so there are no stickers left over?

The sticker problem has to do with the concept of the least common multiple (LCM). (The answer is she should buy 12, 24, 36, or any other multiple of 12 stickers, because then she can divide them either into 4 bags or 6 bags.)

Sure, the problem is VERY unclear and poorly worded. My guess is that the booklet this appears in is simply unedited. It's not the fault of the standards themselves. I agree with Bart Goddard on Math Forum. This is a symptom of the blind rush to produce "real-life" story problems that end up being nonsensible.

From the PDF document it appears in, I conclude the problem is for fourth grade, because all the other word problems in the booklet match standards for 4th grade (factors, primes). But, the CCS don't even include the least common multiple in 4th grade standards (it's in the 6th)!! Something went really haywire with that word problem.

Example 3

Again, supposedly from Houghton Mifflin for 1st grade. This matches the standard I already quoted above:

Add and subtract within 20.
1.OA.6.
Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decomposing a number leading to a ten (e.g., 13 − 4 = 13 − 3 − 1 = 10 − 1 = 9); using the relationship between addition and subtraction (e.g., knowing that 8 + 4 = 12, one knows 12 − 8 = 4); and creating equivalent but easier or known sums (e.g., adding 6 + 7 by creating the known equivalent 6 + 6 + 1 = 12 + 1 = 13).

Now, first of all, the strategy of "making ten" has to do with ADDITION, not subtraction. In subtraction, it is called "decomposing a number leading to a ten". So the instructions should say, "Which shows a way to decompose a number leading to a ten?" I feel it is utter NONSENSE to require 1st grade students to know such terminology.

But there's another problem here. If you actually read all of the standards, you will notice that in several other places it asks students to explain the reasoning used or to relate a certain visual method to the strategy, but NOT in this standard!

The way I see this standard is that teachers are supposed to TEACH the various trategies mentioned and then give students SIMPLE addition and subtraction problems within 20 such as 15 − 8 and 10 − 6. I do NOT see this standard requiring students to recognize if a certain visual model matches a certain strategy.

Again, it looks like the author throws out common sense... and does not actually understand the standards.

Example 4

The example below is very poorly worded but the CONCEPT behind it is very good and is also found in Math Mammoth. I can therefore figure out what they want.

You see five squares. Color some blue and the rest red. That's clear.

Then color the squares in the "number bond" the same way. The number bond goes to those three circles. A child that has been present in a lesson where the teacher teaches number bonds hopefully knows what it means. It's the same concept as a fact family... the top number is the sum or the total (5), and the numbers that go to the bottom circles correspond to how many you colored blue and how many red, in this case 1 and 4.

Then I think the hidden partners are also the 1 and 4. Show 1 and 4 fingers to an adult. Lastly color 1 and 4 fingers in the picture (and not your own fingers like it sounds like).

In my opinion the part about fingers is superfluous and confusing. However, the concept of number bonds is way older than the CCS. Number bonds are actually not mentioned in the CCS, though they do tie in with this standard:

1.OA.4
Understand subtraction as an unknown-addend problem. For example, subtract 10 − 8 by finding the number that makes 10 when added to 8.

and with this one

1.OA.6.
Add and subtract within 20, demonstrating fluency for addition and subtraction within 10.

I don't know why that number bond worksheet is given as an example of Common Core Math. It would be much better titled as an example of poorly worded math worksheet that COULD even date to pre-common core (and is just re-used in this particular curriculum)... because like I said, number bonds are NOT mentioned in the CCS.

What Common Core Math Standards are not

1. They are not "new math." Compared to many math curricula used in the 2000s that were emphasizing non-traditional algorithms, CCS is a clear move towards traditional algorithms and memorization. Check out these specific standards:

   2.OA.2
   Fluently add and subtract within 20 using mental strategies. By end of Grade 2, know from memory all sums of two one-digit numbers.
   
   Maria's note: these are your basic addition facts, such as 7 + 7 or 5 + 4.

   3.OA.7
   Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
   
   Maria's note: this means multiplication tables and basic division facts.

   4.NBT.4
   Fluently add and subtract multi-digit whole numbers using the standard algorithm.

   5.NBT.5
   Fluently multiply multi-digit whole numbers using the standard algorithm.
   
   Maria's note: this does not mean that students multiply multi-digit whole numbers only in 5th grade; that is studied also in 3rd and 4th grades.



2. The standards do not impose strange strategies or visual models on teachers and students. Many standards leave it up to the teachers and students. For example:

   2.NBT.5
   Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.

   Notice the "and/or" in the above sentence. This means the teachers and students are NOT limited to using any specific strategies nor told to use several strategies. The traditional "borrowing" algorithm is a strategy based on place value so it is included right here in 2.NBT.5.

   
   

   2.NBT.9
   Explain why addition and subtraction strategies work, using place value and the properties of operations. Explanations may be supported by drawings or objects.

   It says "may be supported by drawings" but it does not force you to do so, nor limit you to using a specific visual model or type of drawing.

   
   

   3.OA.3
   Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.

   The student does not HAVE to use a drawing. That is just mentioned as a possibility.

   
   

   4.NBT.5
   Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.

   Notice the "and/or". Illustrate the calculation but it's sufficient to illustrate it using equations. You do not HAVE to illustrate it using arrays.

   That said, some standards do mention a specific visual model, such as a number line or rectangular area model but that is less common than giving a choice like in the standards above.

Conceptual math

There are some standards that get into the conceptual side of mathematics that elementary school teachers may not understand if they are not taught what they mean; for example:

5. NF.7b
Interpret division of a whole number by a unit fraction, and compute such quotients. For example, create a story context for 4 ÷ (1/5), and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that 4 ÷ (1/5) = 20 because 20 × (1/5) = 4.

One such story problem would be: how many pieces that are 1/5-ft long can you cut out of a 4-ft piece of material? A visual model could show 4 wholes, divided into fifths. We can then count that 4 wholes have a total of 20 fifths.

5.NF.4b
Find the area of a rectangle with fractional side lengths by tiling it with unit squares of the appropriate unit fraction side lengths, and show that the area is the same as would be found by multiplying the side lengths. Multiply fractional side lengths to find areas of rectangles, and represent fraction products as rectangular areas.

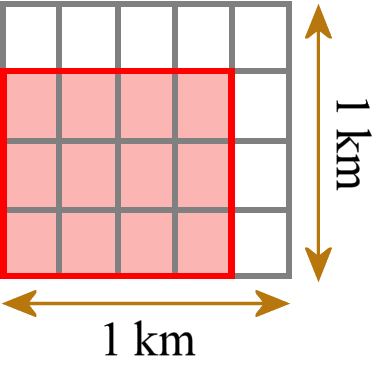This means for example a rectangle with side lengths 3/4 km and 4/5 km. Then we tile it with little unit rectangles (not unit squares; here the standard itself has the wrong terminology) that each have side lengths 1/4 km and 1/5 km.

We can count how many little tiles we need. We need 12 such tiles. Each tile has an area of 1/20 km², so the total area is 12/20 km². Then we check and compare that we get the same answer as if we had multiplied the two side lengths using regular fraction multiplication (3/4 km × 4/5 km  =  12/20 km²).

I have always had these kinds of problems in my books—even before CCS came along.

---

Some people argue that children don't need such conceptual understanding or that it is too difficult. Personally, I disagree. I have always (also before the CCS) striven to explain the concepts of fraction arithmetic so that students don't end up "blindly following the rules", only able to calculate with fractions if they happen to remember the rule correctly. I have always emphasized the conceptual understanding in mathematics (as my readers know!).

But, I hope you can see how some of these things can be unfamiliar to school teachers and parents, and therefore it is no wonder that following Common Core Standards is difficult for them.

It is my hope that Math Mammoth Light Blue Series and the units I sell at my Teachers Pay Teachers store can help those teachers & parents who need Common Core aligned materials. And like I said, the rest of you can be confident in using them as well. They don't contain any "strange" or nonsensical math, but as always, are simply based on the solid foundation of teaching the concepts of math along with the procedures.

Math Mammoth Tour Confused about the different options? Take a virtual email tour around Math Mammoth! You'll receive: An initial email to download your GIFT of over 400 free worksheets and sample pages from my books. Six other "TOURSTOP" emails that explain the important things and commonly asked questions concerning Math Mammoth curriculum. (Find out the differences between all these different-colored series!) This way, you'll have time to digest the information over one or two weeks, plus an opportunity to ask me personally about the curriculum. A monthly collection of math teaching tips & Math Mammoth updates (unsubscribe any time) Email: Receive the emails... Once a day Every 2 days We respect your email privacy. Note: You will FIRST get an email that asks you to confirm your email address. If you cannot find this confirmation email, please check your SPAM/JUNK folder.

"Mini" Math Teaching Course This is a little "virtual" 2-week course, where you will receive emails on important topics on teaching math, including: - How to help a student who is behind - Troubles with word problems - Teaching multiplication tables - Why fractions are so difficult - The value of mistakes - Should you use timed tests - And more! You will also receive: A GIFT of over 400 free worksheets and sample pages from my books right in the very beginning. A monthly collection of math teaching tips & Math Mammoth updates (unsubscribe any time) We respect your email privacy. Note: You will FIRST get an email that asks you to confirm your email address. If you cannot find this confirmation email, please check your SPAM/JUNK folder.

Maria's Math Tips Enter your email to receive math teaching tips, resources, Math Mammoth news & sales, humor, and more! I tend to send out these tips about once monthly, near the beginning of the month, but occasionally you may hear from me twice per month (and sometimes less often). Peek at the previous tips here. You will also receive: A GIFT of over 400 free worksheets and sample pages from my books. We respect your email privacy.