Maria's Math News, November 2023

Hello again!!!

Math Mammoth news
What about grading?
A basic principle of math teaching: Remember the Goals
Division with remainders (grades 3-5)
Just for fun!

1. Math Mammoth news

I will soon run my traditional Thanksgiving sale... starting in a week.

One of my customers wrote in and said, "My daughter wanted to share her line graph with Ms. Maria from grade 4-A line graph lesson number 6 🙂."

She's a happy camper! I love it when kids love their math work!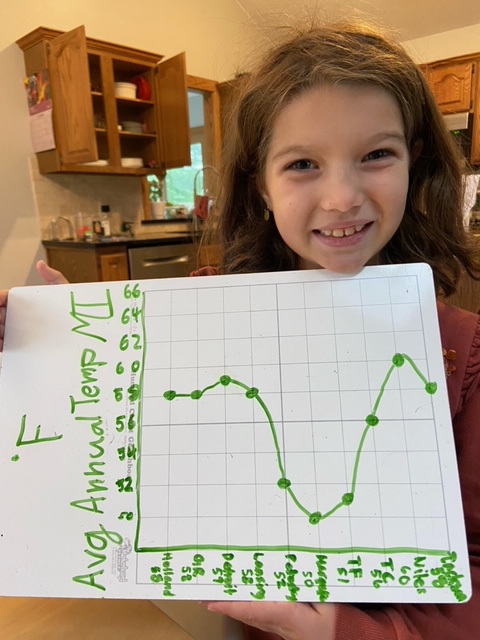

2. What about grading?

Someone asked about GRADING. Here are my thoughts.

In Math Mammoth curriculum, there is a grading chart for the end-of-chapter tests, but MM does not provide grading guidance for individual lessons.

In fact, I don't want to encourage grading individual lessons with numbers/percentages on a continual basis. It can leave a wrong impression in a child's mind that mathematics is supposedly all about "getting correct answers".

Instead, we should approach math work as a process of learning, a process of going through some challenges, working hard, and overcoming through work and persistence. When a child does that, you can praise them with "You worked hard and you did it!"

I also advise parents to AVOID praising a child's intelligence. It has a subtle counterproductive effect (that has been found to be there in scientific studies). It goes like this: A child is praised as being smart/intelligent whenever the child gets something right. The child starts believing they're smart.

Then a challenge comes along. Such children will learn to SHY AWAY from challenges because they FEAR that they will be found to NOT be smart if they cannot do the challenging problem. So, they give up quickly or don't even try.

The sad thing is, then they don't learn to be persistent and to work hard.

It's also been found that instead of giving a child numerical grades (like 10/15), if a teacher WRITES a personal note about "I see you worked hard! Good job!" or similar, THAT encourages the child much more than a numerical grade.

See also: Growth mindset & how to (and how NOT to) praise our students

3. Principle 2: Remember the Goals

This is another habit or basic principle of effective math teaching. 😃

What are the goals of your math teaching? Are they...

to finish the book by the end of school year...?
make sure the kids pass the test...?

Or do you have goals such as:

My student can add, simplify, and multiply fractions;
My student can divide by 10, 100, and 1000.

These all are just "subgoals". But what is the ULTIMATE GOAL of learning school mathematics?

Consider these goals:

Students need to be able to navigate their lives in this ever-so-complex modern world. This involves dealing with taxes, loans, credit cards, purchases, budgeting, and shopping. Our youngsters need to be able to handle money wisely. All that requires good understanding of fractions, decimals, and percents.
Another very important goal of mathematics education as a whole is to enable the students to understand information around us. In today's world, this includes quite a bit of scientific information. Being able to read it and make sense of it requires understanding of big and small numbers, statistics, probability, and percents.

And then one more. We need to prepare our students for further studies in math and science. Not everyone ultimately needs algebra, but many do, and teens don't always know what profession they might choose or end up with.
I'd like to add one more broad goal of math education: teaching deductive reasoning. Naturally, high school geometry is a good example of this, but when taught properly, other areas of school math can do it as well.

The more you can keep these BIG REAL goals in mind, the better you can connect your subgoals to them. And the more you can keep the goals and the subgoals in mind, the better teacher you will be.

For example, adding, simplifying, and multiplying fractions all connects with a broader goal of understanding parts and whole. This will then lead to ratios, proportions, and percent. Another example: the mastery of all fraction operations is necessary for solving rational equations and manipulating rational expressions in algebra courses.

Tying in with the goals, remember that the BOOK or CURRICULUM is just a tool to achieve the goals — not a goal in itself. Don't ever be a slave of any math book!

4. Division with remainders

A few years ago, one of my users was stumped by this problem...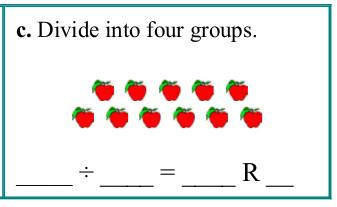

There is a picture of 11 apples and it says to "Divide into four groups." Now, 11 ÷ 4 = 2 R3. (We get two apples in each group, and three apples left over.) Here comes the part that stumped this customer:

"...if I divide 11 into 4 groups, the groups have to be 2. That leaves a remainder of 3, but then the remainder is bigger than the group. It seems like it could be right anyway, but if you "check" the answer by using 11 ÷ 2, you get 5 R1."

In other words, they felt that 11 ÷ 4 = 2 R3 is correct, but that the check, 11 ÷ 2, fails, because you get 5 R1.

This is an interesting question! There are a few things to keep in mind:

Remainder problems are not checked that way (by using the quotient as the divisor). Instead, you multiply and add. For example, to check 23 ÷ 6 = 3 R5, multiply 3 × 6 and then add the remainder 5. You should get the original dividend.

In the case of this problem, 11 ÷ 4 = 2 R3 is checked by 2 × 4 + 3, which does equal 11, the dividend.

Then also, let's think about this statement: "That leaves a remainder of 3, but then the remainder is bigger than the group."

Here, we need to keep in mind:

The DIVISOR in division problems can be interpreted to mean two different things: either the number of groups OR the amount in each group.
The rule is: the remainder should not be more than the divisor. It is not that the remainder should not be more than the "group". If you think of the point (1) above, you are either interpreting the division problem as "division into certain size groups", or "division into certain amount of groups".

In this case, we have 11 apples to be divided into four groups. The divisor is 4, and it means the number of groups. We get 11 ÷ 4 = 2 R3. The remainder of 3 is NOT more than the divisor (4), so everything is fine! If we had 4 apples left over, we could give each group one more apple, but we have only 3 left over, so we can't.

Taking the division 11 ÷ 2 = 5 R1, using the same interpretation, we'd be dividing into TWO groups. That is not going to check the division 11 ÷ 4, where 11 are divided into four groups. The check is always simply to multiply the divisor and the quotient, and add the remainder — and you should get the dividend.

5. Just for fun!

Thanks for reading! 🙂

Feel free to forward this issue to a friend/colleague! Subscribe here.

Till next time,
Maria Miller