Hello again!!!
|
1. Math Mammoth newsI'm working consistently on the 8th grade curriculum — right now on the answer key, mixed reviews, and in collaboration with my son, the worksheet maker.Here's a glimpse to what I've been working on... for the chapter on bivariate data where students will study scatter plots and two-way tables.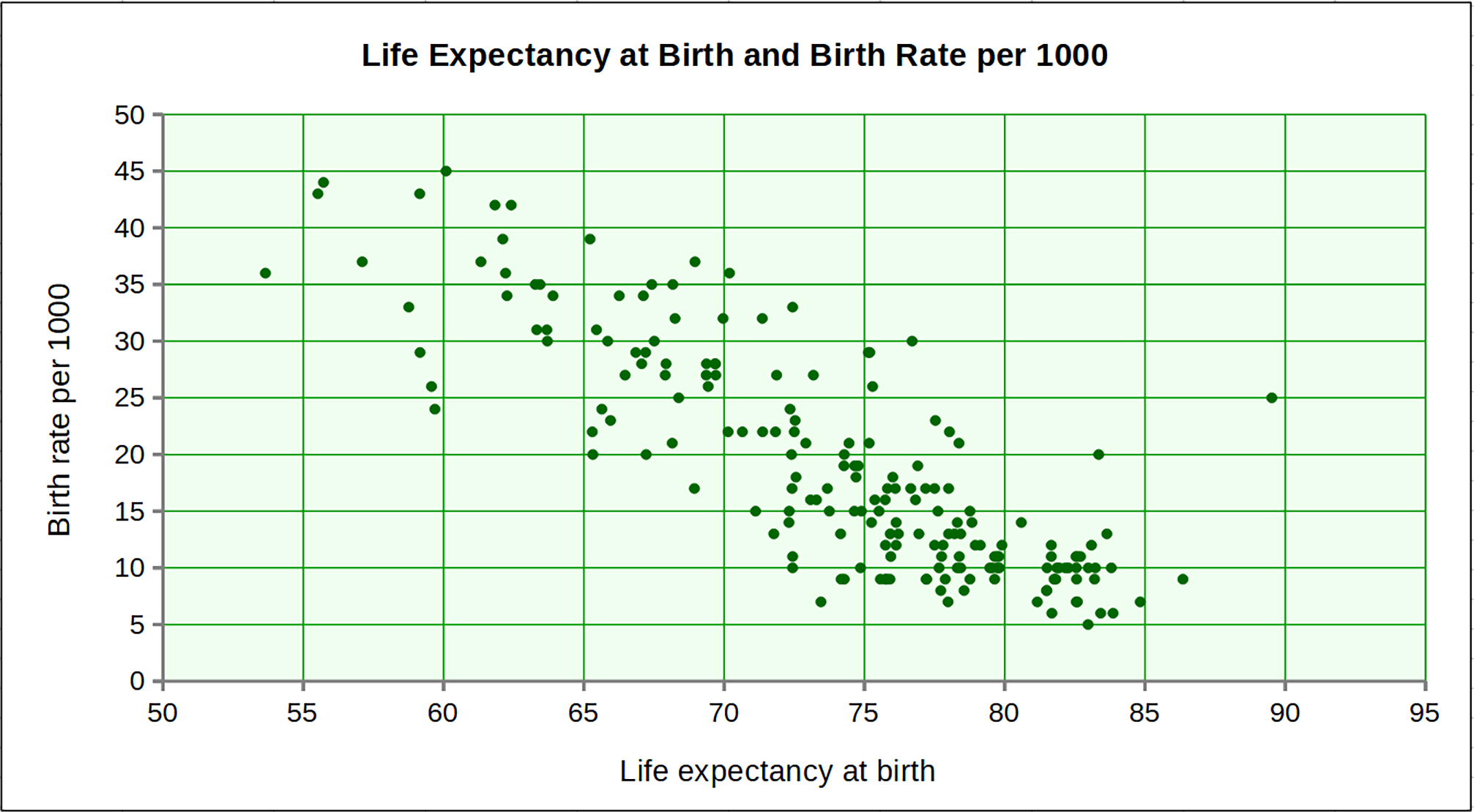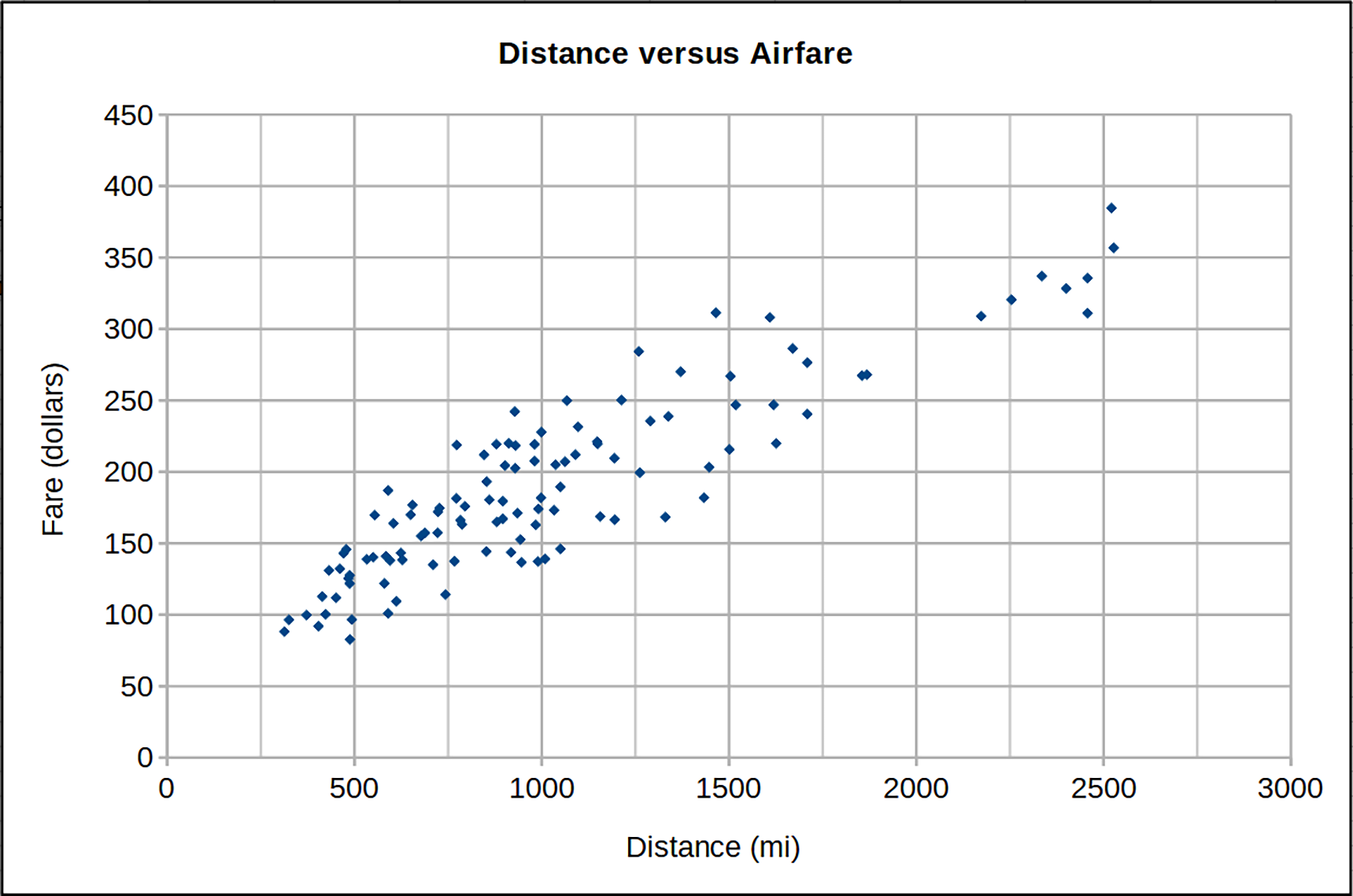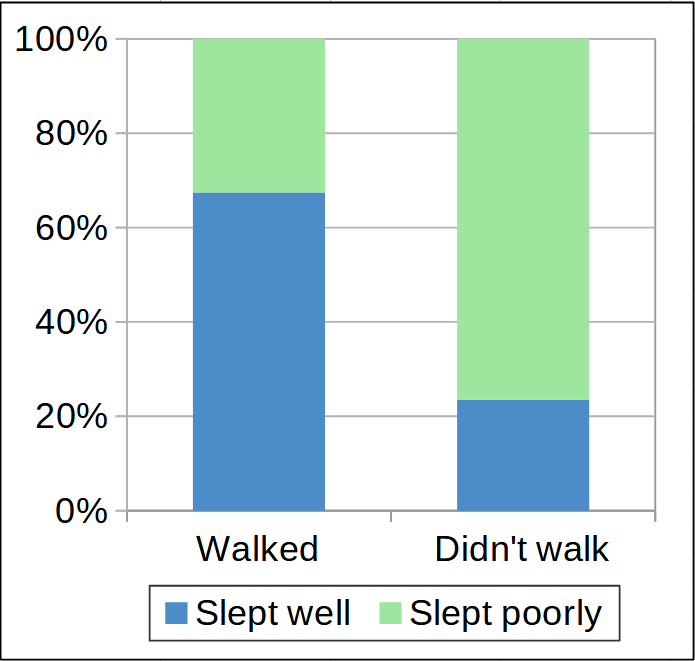   
Making problems for statistics is often challenging for me, since I have to research to find data, OR make it up but in a believable manner, and then format the graphs so they're visually clear. And also, that the numbers are feasible to work with if there will be calculations. And not only all that, but use topics that are (hopefully) not sensitive or boring, or influence young people in a wrong manner. But it's interesting, too, and I figure students will enjoy statistics as a topic because of its many ties to real life. As an example, I saw many examples of math problems where it showed categorigal data... students divided by age into categories such as 13-14 year olds and 15-16 year olds, etc. and then as the other variable, whether they had a cell phone or not. I considered it but decided not to include one on that topic, because families have many differing opinions on that issue. So, it sometimes feels tricky and I'm sure the presentation is not perfect but I did try to make it as good as I could. Grade 5 Canadian version is now available in print, not only at Lulu, but in various bookstores including Amazon. Use these ISBN numbers: Grade 5-A Worktext, Canadian Version 978-1-954358-40-9The ones at Lulu are probably cheaper though. All the options are listed on our printed books page. Someone sent in this tip: When my oldest used Math Mammoth, her math 'warmup' for the day was to find 5-10 incomplete problems from prior lessons. It was a great way to get her brain going & add a little review before we tackled that day's lesson. |
2. The times tables — interactively!Check out my interactive multiplication course at TinyTap! You will get access to 20 interactive lessons that contain videos and interactive exercises. Some lessons focus on a particular multiplication table, while others are for reinforcing earlier concepts and skills. The lessons contain not only simple practice, but also word problems, puzzles, and other types of multiplication exercises. See a free example lesson from the course: The Multiplication Table of 5 Here are a few other resources for the tables: 
|
3. A basic principle of math teaching: Let It Make SenseIf you were asked what were the most important principles in mathematics teaching, what would you say? I wasn't really asked, but I started thinking, and came up with these basic habits or principles that can keep your math teaching on the right track.
Principle 1: Let It Make Sense
Principle 2: Remember the Goals Principle 3: Know Your Tools Principle 4: Living and Loving Math Let's look at each of those in more detail. Principle 1: Let It Make SenseLet us strive to teach for understanding of mathematical concepts and procedures, the "why" something works, and not only the "how".This understanding, as I'm sure you realize, doesn't always come immediately. It may take even several years to grasp a concept. For example, place value is something kids understand partially at first, and then that deepens over a few years. 
This is why many math curricula use SPIRALING: they come back to a concept the next year, and the next (and the next and the next...). Or, some curricula come back to a concept sooner than that... maybe every two weeks or so. Now, spiraling can be very good if not done excessively. Unfortunately, some math curricula spiral concepts over so many years, and in such little pieces at a time, that they never teach the concepts and ideas in depth. Then some others have a "tight" spiral where each concept is revisited every few weeks, which then causes MOST of each lesson to be review problems — again causing a lack of focus and lack of depth. Spiraling also presents this pitfall: it can cause parents/teachers to blindly "trust" the spiraling and think, "Well, he didn't get it this year... but he'll get it next year when the book comes back around to it." However, the presentation of that concept in the next year's schoolbook might be too difficult for such a child. When it comes to spiraling, we need a BALANCE. Children do need review, but they also need a chance to focus on major concepts and get a fairly full picture of connecting thoughts (the depth). The "how" something works is often called procedural understanding: the child knows HOW to work long division, or the procedure of fraction addition or fraction division, for example. 
It is often possible to learn the "how" mechanically without understanding why it works. Procedures learned this way (via rote memory) are also often forgotten very easily!That is why in my Math Mammoth curriculum I have focused on the conceptual understanding so much. The child might learn the "HOW" quicker than he will learn the "WHY", but learning only the "HOW" will cause him to easily forget what has been learned. Plus, that will not help the child to learn to reason and make connections in mathematics. The relationship between the "how" and the "why" — or between procedures and concepts — is complex. One doesn't always come totally before the other, and it also varies from child to child. You can try alternating the instruction: teach how to add fractions, and let the student practice. Explain why it works. Go back to some practice. Back and forth. Sooner or later it should 'stick' — but it might be next year instead of this one, or after 6 months instead of in this month. As a rule of thumb, don't totally leave a topic until the student both knows how, and understands the 'why'. Tip: you can often test a student's understanding of a topic by asking him to PRODUCE an example, preferably with a picture or other illustration: "Tell me an example of multiplying fractions by whole numbers, and draw a picture." Whatever gets produced can tell the teacher a lot about what has been understood. |
4. Thoughts about algebra 1
It's updated and simplified, and hopefully will help everyone to navigate the decision as to where to go after Math Mammoth 7 or 8. |
5. Just for fun!
Thanks for reading! 🙂 Feel free to forward this issue to a friend/colleague! Subscribe here. Till next time, Maria Miller |
| Complete curriculum | Math games and interactive practice | Math Mammoth freebies | New to MM? Start here |
| Privacy & your personal data | The Challenge | Blue Series: For filling in gaps |