Hello again!!!
|
1. Math Mammoth newsHere are photos of our new BROCHURE that is currently being sent to some homeschool conventions, for their "welcome bags". 😃   Both digital and print versions are available. Contents and samples: Grade 5-A samples Grade 5-B samples Emily, one of my customers, sent in this photo from their Pi day celebration (3/14): These Math Mammoth students used their recently-learned fractions skills to make a Pi Day pie! 1st grader was able to find the appropriate measuring cups and spoons for the recipe, and 4th grader was able to calculate the amounts for a single pie from a doubled recipe!  |
2. Beach Comparisons game
Children will have fun comparing numbers and numbers of objects on the beach! Choose from three game modes:
Check it out! |
3. What does this pattern remind you of?A customer sent this picture to me. It's an exercise from MM 4-A.Great thinking, connecting the pattern with real life! Now, we might not want to ride with this kid driving... however, maybe he is thinking of an airplane! 😄  |
4. What to do after MM7Someone asked about what to do after MM7:"My son has completed math mammoth 7th grade. What curriculum do you recommend for 8th grade math?"Right now you have the option of actually doing some more Math Mammoth materials, because I'm in the process of writing 8th grade level materials. These materials are being published as topical units in our Blue Series, and the following are already published: Exponents and Scientific Notation — grades 8-9. Negative and zero exponents, exponent laws, significant digits, scientific notation, using scientific notation in calculations. Geometry 4 — grade 8. Congruent transformations, dilations, angle relationships, volume of pyramids, cones, spheres, and cylinders.  Introduction to Functions — grade 8. Concept of a function, rate of change, linear and nonlinear functions, modeling with linear functions, describing functions, comparing functions. Graphing Linear Equations — grades 8-9. Comparing and graphing proportional relationships, slope, slope-intercept equation, horizontal & vertical lines, standard form, parallel & perpendicular lines. The other option is to go to Algebra 1, such as with the textbooks & companion products from mathwithoutborders.com. See also some other options listed here. The choice between going directly to algebra 1 and the new MM8 basically boils down to this: if your son did well with MM7, he could go to algebra 1. If instead you feel he would benefit from a slower pace with algebraic concepts, he could do the books I have for 8th grade, and then go on to high school math. 😀 |
5. Polykite hatMath news: A 13-sided shape known as “the hat polykite” has mathematicians tipping their caps.😀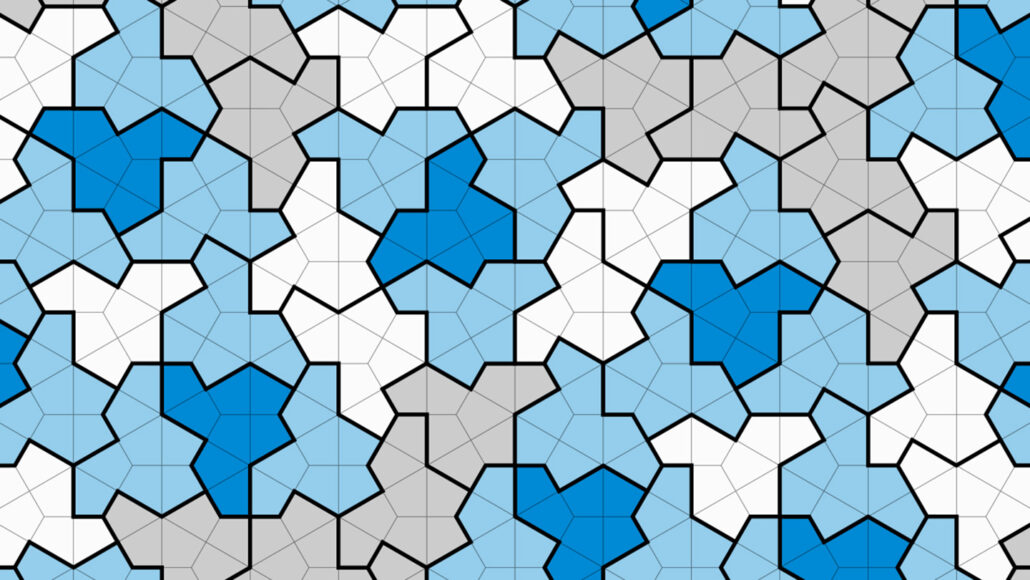 A 13-sided tile called “the hat” forms a pattern that covers an infinite plane yet it cannot repeat, making it a long-sought shape known as an “einstein.” D. Smith, J.S. Myers, C.S. Kaplan and C. Goodman-Strauss (CC BY 4.0) This shape looks like a hat, and is made up of several kite shapes. It has an extraordinary property: it is what mathematicians call an "einstein": a shape that can tile the plane, without any repeating pattern. Mathematicians have finally discovered an elusive ‘einstein’ tile On this site, you can play around with this shape in an interactive app to form such tilings yourself: Aperiodic monotiles exist! |
6. Just for fun!
Thanks for reading! 🙂 Feel free to forward this issue to a friend/colleague! Subscribe here. Till next time, Maria Miller 
|
| Complete curriculum | Math games and interactive practice | Math Mammoth freebies | New to MM? Start here |
| Privacy & your personal data | Mining Spiritual Gold | Blue Series: For filling in gaps |