Maria's Math News, October 2020

Hi again!

I hope you enjoy this month's newsletter items!

Math Mammoth news
Resources for addition & subtraction facts (grades 1-3)
Divide decimals by decimals (grades 5-8)
The most important question you should ask in mathematics
Mathy's Berry-Picking Adventure (grades 1-4)
Math puzzles for all ages
Just for fun!

1. Math Mammoth news

Another testimonial... 😊

Ms. Miller,
I just wanted to write to say how pleased I am with your math program. This is our first year homeschooling. I bought Light Blue 1A and 1B for my twin first graders and 2A and 2B for my second grader. All 3 of my children's math skills have gone up so much since starting in August. My second grader now has his addition facts to 18 down from memory and no more counting on his fingers. He loves the tips and tricks for remembering those facts. He is excelling in every part, but this is what we are on now so it is just blowing me away.

My first graders of course missed half of kindergarten due to COVID 19 and had no concept of adding or subtracting starting the year out. Needless to say, I was so nervous to homeschool them. Now, they have finished addition facts to 10 and are on subtraction and it is coming so easy. They are remembering the facts now and are able to add numbers bigger than 10 with no problems. Same with subtraction. I am just so pleased with your product. It has made teaching math easy, and so uncomplicated (this is coming from someone who hated math in school)... I have even used some of the mental math tricks for myself! Haha

Also I love that it is common core aligned if one day they do return to public school, they are on the same page as the school system.

Just wanted to give you some very positive feedback.

Thanks so much,
Breanna Hall

2. Resources for addition & subtraction facts

Many customers ask about addition and subtraction facts, so I finally made a page that lists the main resources I offer for them all in one place – videos, games, online practice, and books.

Addition and subtraction facts are fairly important to learn in the early years of elementary school, because knowing those facts is a big factor in developing number sense – the ability to work with numbers flexibly.

For example, once you have learned by heart that 6 + 6 = 12 or that 7 + 8 = 15, then sums such as 60 + 60 or 700 + 800 are as easy as pie.

Furthermore, you can use basic addition and subtraction facts to help you with many other problems.

Here's another example... you can solve 76 + 6 by using your knowledge of 6 + 6 = 12. 76 + 6 is 70 plus 6 + 6. Or think this way: 76 + 6 must be in the 80s and end in 2, just like 6 + 6 = 12 ends in 2.

Check out the resources here!

3. Looking back... 10 years ago

I've written a newsletter now for 14 years. (The first one was in August 2006.) Here's an excerpt from 10 years ago... 2010. It is mind-boggling how fast time flies!

This entry is about dividing decimals by decimals – and of course math concepts and skills don't change; they are as fresh as ever!

When dividing decimals by decimals, such as 45.89 ÷ 0.006, we are told to move the decimal point in both the dividend and the divisor so many steps that the divisor becomes a whole number. Then, you use long division. But why?

Schoolbooks often don't tell us the "why", just the "how".

This video explores this concept.

[This is a REALLY old video of mine... you can see how I looked like in my younger years! We used a camera that took little tiny disks, didn't have good lighting, and I was nervous. :) The same concept is also taught in this newer video of mine. ]

It has to do with the fact that when we move the decimal point, we are multiplying both numbers by 10, 100, 1000, or some other power of ten. When the dividend and the divisor are multiplied by the same number, the quotient does not change. This principle makes sense:

0.344 ÷ 0.004 can be thought of, "How many times does four thousandths fit into 344 thousandths?"

The same number of times as what four fits into 344!

So, 0.344 ÷ 0.004 can be changed into the division problem 344 ÷ 4 without changing the answer. Both 0.344 and 0.004 got multiplied by 1000.

When we simplify fractions or write equivalent fractions, we use the same principle. Remember, fractions are like division problems.

3/7 is 3 ÷ 7.

And, 3/7 = 6/14. We can multiply the numerator and the denominator (or the dividend and the divisor) by some same number, without changing the value of the fraction (the quotient).

Or, 90/100 = 9/10. Or 0.9/0.2 = 9/2.

4. The most important question you should ask in mathematics

Some of you might enjoy this article...

I'll spill the beans... the question she's talking about is, "Why did you say __________?" 🙂

It initiates a conversation about what the student or child is thinking, and WHY they're doing what they're doing in the math problem.

Sometimes we are too eager to get into the right answer. It's important to listen to the reasons the child has for doing what they did. Math isn't just about the correct answers. It also has to do with reasoning and with problem solving as a process.

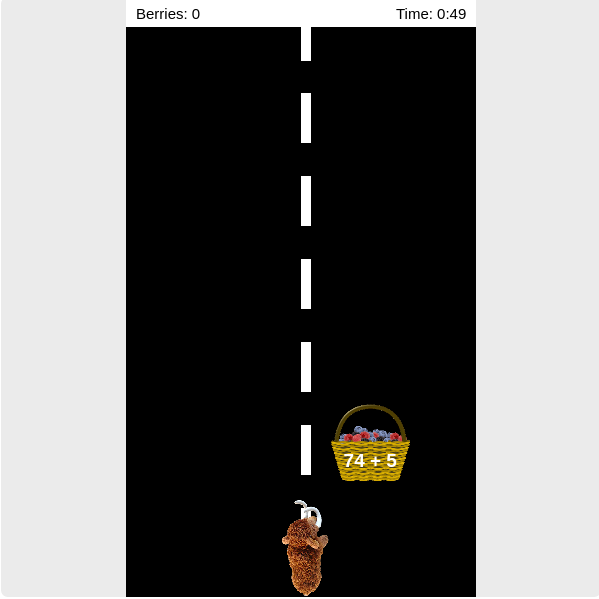
5. Mathy's Berry-Picking Adventure

A new game at Math Mammoth Practice! Join Mathy (our mammoth mascot) on his berry-picking adventure, and practice your mental math! You can choose to practice single-digit or double-digit addition or subtraction, or multiplication tables. You get 100 berries (points) for every correct answer, and lose 50 for every wrong answer.

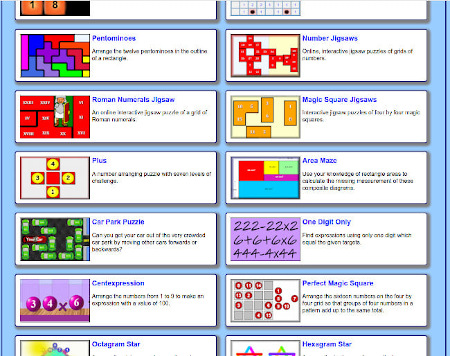
6. Math puzzles for all ages

Time for math puzzles? LOTS of choices... mathematical concepts for all levels. 😊 Check them out here!

7. Just for fun!

Thanks for reading!

Feel free to forward this issue to a friend/colleague! Subscribe here.

Till next time,
Maria Miller