Maria's Math News, March 2020

Hello again!

Math Mammoth news
How does Math Mammoth teach math facts? (grades 1-4)
Interactive sieve of Eratosthenes (grades 4-12)
Teaching word problems (grades 1-12)
"How to Learn Math" (for students) (grades 1-12)
The equals sign creates trouble
Just for fun!

1. Math Mammoth News

Here's a short video I recently recorded covering the basics of Math Mammoth curriculum:

Math Mammoth will be at Homeschool Connect Expo March 25-29 – this is an online expo that is completely free to attend!

I will soon (mid-March)run a sale at the MathMammoth.com website. Stay tuned!

Someone asked recently about 8th grade math.

...does that mean that students who've graduated from MM 7 can go straight into algebra? Or, should they use another gr. 8 math curriculum, first? In your opinion, how much of a gap is there in content between MM 7 and algebra?

Many of you may already know the answer... Math Mammoth Grade 7 is designed to be a pre-algebra curriculum, so after completing MM7, students can continue to algebra 1 or some other high school math course.

This also allows you some flexibility. If your child or student is going to start high school math in grade 9, you could choose to spread out MM6 + MM7 to, say 2.5 years, or whatever you feel comfortable with. That would then leave the student an extra 1/2 year to spend with algebra 1, or just to take a break.... 😄

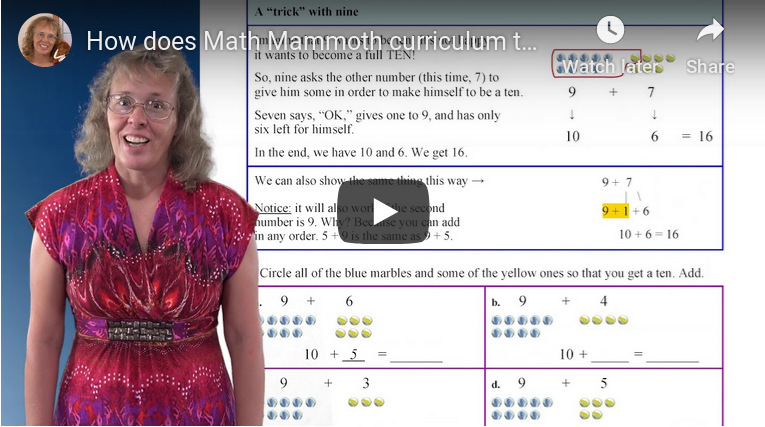
2. How does Math Mammoth teach math facts?

Math Mammoth uses a hybrid approach where the children are shown various strategies for math facts, but the curriculum also incorporates some drill.

For addition and subtraction facts, the main or foundational strategy is that of fact families. We don't just study one fact family here and there, but GROUPS of fact families. The reason for that is, it allows the child to see the PATTERNS and the structure in these facts. But – we also use drills. (See an example video here.)

There are also other strategies taught, such as doubles plus one, and the nine-trick.

For multiplication tables, the curriculum incorporates what I call a structured drill. This consists of first memorizing the skip-counting pattern, which are the answers, and then associating the different multiplications with the answers. At first the drilling is done within the structure of the table, and not randomly. From that we upgrade to random drilling.

The tables are also taught in a very specific order which lessens the overall memorization work. And there are videos that you can use for the multiplication table drills.

Based on the feedback I've gotten, this approach has proven to be quite effective.

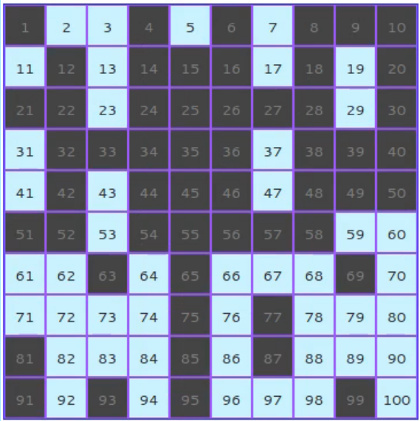
3. Interactive sieve of Eratosthenes

CodeLover made an interactive sieve of Eratosthenes for finding prime numbers... 😄 It's kind of fun to play with!

4. Teaching word problems

Someone recently asked me these two questions:

1. Do you have a book on just teaching word problems?

2. Do you have a list of key words that signal what action to take in a word problem?

No, I don't have a book focusing on word problems only... but some day we might put together one.

And I don't have a list of such keywords either. In fact, I don't believe in such an approach. Typically, if you teach that "this" word signals a certain operation, one can devise a wording where that same keyword signals something else.

For example, "more". Does it always signal that you should add? Consider this one:

Mickey has some toy cars, and Henry has 9, which is five more than what Mickey has.

Of course, most of you probably know that Math Mammoth books contain plenty of word problems. If a child has difficulties with them, I suggest, first of all, starting from the beginning, and secondly, asking children to draw or act out the word problems with objects, in grades 1-3 in particular. If the child continues have lots of difficulties, you might check if they have any problems with reading comprehension.

This article of mine can also help: The trouble with math word problems.

5. "How to Learn Math" (for students)

The course "How to Learn Math (for students)" from Youcubed/Jo Boaler is now available for free from edX.

I have gone through this course several years ago and my daughters have as well; it is a good one. The goal is not so much to learn math per se, but to gain a different mindset towards math.

Here's the syllabus:

Part 1: The Brain and Math Learning
1. Knocking Down the Myths About Math

Everyone can learn math well. There is no such thing as a “math person”. This session give stunning new evidence on brain growth, and consider what it means for math learners.

2. Math and Mindset

When individuals change their mindset from fixed to growth their learning potential increases drastically. In this session participants will be encouraged to develop a growth mindset for math.

3. Mistakes and Speed

Recent brain evidence shows the value of students working on challenging work and even making mistakes. But many students are afraid of mistakes and think it means they are not a math person. This session will encourage students to think positively about mistakes. It will also help debunk myths about math and speed.

Part 2: Strategies for Success
1. Number Flexibility, Mathematical Reasoning, and Connections

In this session participants will engage in a “number talk” and see different solutions of number problems to understand and learn ways to act on numbers flexibility. Number sense is critical to all levels of math and lack of number sense is the reason that many students fail courses in algebra and beyond. Participants will also learn about the value of talking, reasoning, and making connections in math.

2. Number Patterns and Representations

In this session participants will see that math is a subject that is made up of connected, big ideas. They will learn about the value of sense making, intuition, and mathematical drawing. A special section on fractions will help students learn the big ideas in fractions and the value of understanding big ideas in math more generally.

3. Math in Life, Nature and Work

In this session participants will see math as something valuable, exciting, and present throughout life. They will see mathematical patterns in nature and in different sports, exploring in depth the mathematics in dance and juggling. This session will review the key ideas from the course and help participants take the important strategies and ideas they have learned into their future.

Check out the course here.

6. The equals sign creates trouble

Did you know the humble equals sign (=) creates actually a lot of trouble?

I found it interesting that when students were asked to complete this:

4 + 3 + 2 = ( ) + 2

Many students will incorrectly add everything on the left, put that in brackets, then proceed to add the final 2.

4 + 3 + 2 = (9) + 2 = 11

The question really requires the following:

4 + 3 + 2 = (7) + 2 = 9

------------------
Another problem is the "running equals" phenomenon, where people write things like

10 + 4 = 14 + 5 = 19 − 6 = 13

If you take the first and the last expressions in the above "chain", you get 10 + 4 = 13.

According to the article, people in the US have much more of a problem with running equals than people in other countries, and I must say my experience agrees with that. The author of the article was thinking maybe it has to do with the fact children are allowed to use a calculator from a very young age. (Calculators often use "running equals" type of a processing.)

7. Just for fun!

Thanks for reading!

Feel free to forward this issue to a friend/colleague! Subscribe here.

Till next time,
Maria Miller