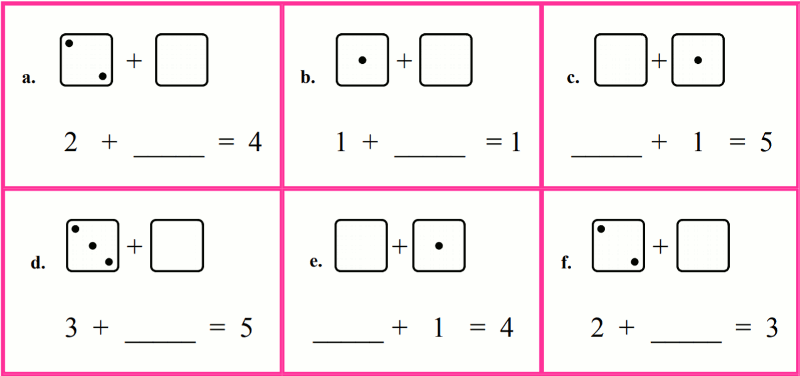Maria's Math News, January 2018

Welcome to a new year!

This newsletter is a bit full so I'm letting you know right here at the top that I will be running a sale in the latter part of January, so stay tuned!

In this edition:
  1. Math Mammoth Light Blue Series — overview
  2. Giveaway! (Brilliant) (grades 4-12)
  3. Missing numbers in addition (grades K-2)
  4. The order of multiplier & multiplicand — does it matter? (grades 3-6)
  5. The problem with Pentagons (grades 5-12)
  6. Number Sense: 7 × 9 (grades 3-12)

1. Math Mammoth Light Blue Series — overview

A NEW video giving you an overview of Math Mammoth Light Blue Series for grades 1-7:



In case you don't know, the Light Blue series is the complete curriculum offered by Math Mammoth, and is the most popular series of Math Mammoth materials. The video explains the basic components of the curriculum, how it can be self-teaching, and thoughts about mastery versus spiraling. I also explain the options for review and where to get started (hint: placement tests).

Brilliant.org problem solving site

2. Giveaway

Here's a brilliant offer (pun intended :))! I've arranged with Brilliant.org to give away:
  • 5 Brilliant Premium subscriptions (worth $96 each).
To take part, click here and sign up for a free account. Your chances of winning are INCREASED each day you do a problem! Winners will be notified by email on January 12.

What is Brilliant.org?

Brilliant is a website that lets you go further into the world of math and science by actively solving problems. They offer mini-courses of short, curated puzzles that provide step-by-step guidance to help develop intuition for the right answers, while pointing out mistakes and misconceptions in the wrong answers.

Selection of courses from Brilliant

Besides math, they also have Physics of the Everyday and computer science. These courses are fun introductions for you and your kids to fall in love with math and science and reinforce your understanding with engaging problems.

Click this link to enter the giveaway by signing up for a free account. And rememeber, your chances of winning are INCREASED each day you do a problem!

Winners will be notified by email on January 12.

Enjoy solving problems! I personally have enjoyed taking a few minute breaks from my regular computer work and solving a few problems there.

3. Missing numbers in addition

Several people have asked me about this... what to do when a 1st grader is struggling to grasp the concept of missing numbers in addition problems, such as 3 + ___ = 8.


This concept comes up quite early in Math Mammoth Grade 1, and it is called "missing addends". You can see some pages from that lesson in the sample file for grade 1, on page 19.

Here's a way to test if a child is ready for that concept.


4. The order of multiplier & multiplicand — does it matter?

Several people have asked me about this topic over the years... here's the basic question:
It seems that in Math Mammoth Multiplication 1 book, the multiplicand is second number and not the first. I had been taught that the equations are multiplicand × multiplier = product. I know that either order will produce the same product but is there a reason that you have the the equations multiplier × multiplicand? Just want to make sure that I am consistent when teaching my son.

In case you don't know, "multiplicand" is the number or quantity we are multiplying, and "multiplier" is the number we multiply by.

Yes, I do have a reason for it. It has to do with what happens down the road a bit.

In 4th grade, students encounter the thought of a fractional part of a quantity, such as finding 3/4 of $36. While we first use a two-step operation to find the answer, eventually (in 5th grade) students will learn how this corresponds to the fraction multiplication ¾ × 36.

Notice how the word "OF" from "3/4 of $36" translates into MULTIPLICATION, and the multiplicand is written SECOND.

Continue reading...

5. The problem with Pentagons

A well-written article (and easy to read even for laypeople) about a century-old math problem that has FINALLY been solved!

It has to do with tiling the plane with PENTAGONS.

In a nutshell, there are only 5 families of convex pentagons that tile the plane. The situation is altogether different, and much easier, for rectangles, triangles, and quadrilaterals.

The article explores and explains these concepts in an easy-to-follow manner and with wonderful graphics. Tilings are something easy to understand, yet when it came to pentagons, the situation turned to be very complex.

At this second link you can see the 15 families of pentagons that tile the plane. Take a peek!

6. Number Sense: 7 × 9

Here's a quick read, and a reminder of a PRINCIPLE of HOW you can calculate 7 × 9 quickly (assuming you don't know it by heart). This is number sense, which is SO important!

(Hint: think of 7 × 10 and how much 7 × 9 lacks from that.)

I do definitely advocate learning the times tables by heart, including 7 × 9, but while your child is learning the facts, you can teach this strategy to him/her... plus the same strategy also applies to other calculations, such as 7 × 99 or 5 × 49, or similar.



Thanks for reading! :)

Feel free to forward this issue to a friend/colleague! Subscribe here.

Till next time,
Maria Miller
Math Mammoth freebies Math Mammoth on Facebook Newsletter Archives
 
Inspire4 Complete curriculum Placement tests








--