Maria's Math News, April 2017 |
|
Welcome to the April edition! In this edition:
1. Math Mammoth news
|
2. Looking back: Ten years agoIn my newsletter 10 years ago...
In case you're interested, you can find the old (and new) newsletters at www.mathmammoth.com/newsletter/ |
3. How to help your kids fall in love with math A
short guide with important points for parents... worth sharing!
A
short guide with important points for parents... worth sharing!
I especially like the third, and last point that emphasized that we adults need to "think out loud", or model our thinking processes — and that is one great way for children to learn math. How to help your kids fall in love with math — a guide for grown ups |
4. A child is not getting addition factsHere's an interesting question concerning a child who's not getting basic addition facts.Hi! I would love some insight and had Math Mammoth recommended to me. My daughter is 7 and in first grade. She is a natural at reading/spelling and is very much a perfectionist. She is not "naturally" mathy. I wasn't either in school and got left behind in math pretty quickly in traditional school. Here's my suggestion... What you can do is to have her study some other topic for a while, and then come back to the addition facts later. For example, study reading the clock, measuring, geometry, money, or place value (2 or 3-digit numbers) for now. Math Mammoth will allow you to do that... it is mastery-based, but since it's organized by topical chapters (one chapter for money, another for measuring, etc.), you can easily choose to "jump around" a bit to give variety, and also for the reason like your situation... to let the child's mind mature, and come back to the "problem topic" later on. Hope this helps! |
5. Math teacher's feelingsPeak into a math teacher's feelings... I definitely agree with many thoughts mentioned in this letter, such as how (in the US) it is seemingly very acceptable to brag about one's lack of basic math skills, which I feel is kind of strange!=> Dear Community; Sincerely, Math Teacher |
6. A different approach to two-column proofs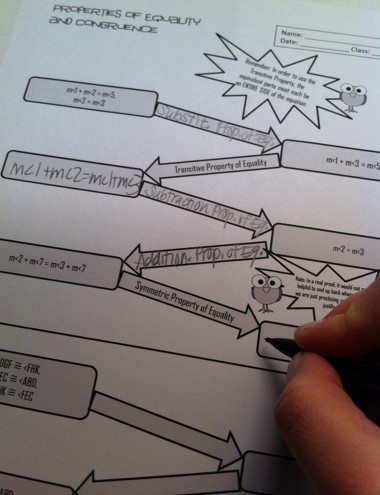 Teaching high school geometry? I assume not many of you are, but if you are, you might be interested in this:
Teaching high school geometry? I assume not many of you are, but if you are, you might be interested in this:
Introducing Two-Column Geometry Proofs: A Different Approach, by Brigid at Math Giraffe website QUOTE: Leading into proof writing is my favorite part of teaching a Geometry course. I really love developing the logic and process for the students. However, I have noticed that there are a few key parts of the process that seem to be missing from the Geometry textbooks. => Read more at Math Giraffe website Thanks for reading! Feel free to forward this issue to a friend/colleague! Subscribe here. Till next time, Maria Miller |
| Math Mammoth freebies | Math Mammoth on Facebook | Newsletter Archives |
| Inspire4 | Complete curriculum | Placement tests |