Review of Geometry: A Guided Inquiry with Home Study Companion by David Chandler
I review here a combo package for high school geometry sold by Math Without Borders, consisting of:
- Geometry: A Guided Inquiry (a textbook);
- Home Study Companion to the textbook, consisting of video lessons, solutions, and Geogebra demonstrations.
- Geogebra dynamic geometry software (free)
While these two will work together, I will describe each part separately in the review. Please use the quick links below to jump directly to the various sections, if you'd like. Naturally, the review about the book is the longest.
The book: Geometry: A Guided Inquiry
How Geometry: A Guided Inquiry handles proof
An axiomatic vs. discovery based geometry text
The Home Study Companion
The software: Geogebra
The book

Geometry: A Guided Inquiry by Chakerian, Crabill, and Stein
Geometry: A Guided Inquiry is a problem-centered textbook. Each chapter starts with a central problem, which acts as a starting point for developing important concepts and theorems.
The text reads like a "worktext": many of the problems are an inseparable part of the overall instruction, because they will lead the student in a step-by-step manner to important theorems and results. This lets students become familiar with the concepts gradually, and the instruction constantly builds upon previous knowledge, just as is normally done in mathematics. (Naturally, the book also contains plenty of exercises that simply practice a concept just presented.)
In essence, the student is guided in his geometrical inquiries by the questions presented, as if a teacher was guiding him by hand. For this reason, I feel this text is an excellent choice for anyone who is studying geometry without a teacher.
Let's look at an example.
An example of how guided exercises lead to a theoremOn page 197, the student first learns and proves that if a point P is equidistant from the endpoints of a line segment, then P is on the perpendicular bisector of the segment.
The very next exercise has a chord AB of a circle with center P, and asks why the perpendicular bisector of AB passes through P. The next part has a picture showing two chords of a circle, and asks where the perpendicular bisectors of the two cords intersect. Another picture with two chords, and a question, "Why must the perpendicular bisectors of the two chords intesect?" The student fills in a sentence: "The perpendicular bisector of a chord passes through the __________ of the circle."
Soon follows a problem with a triangle and the perpendicular bisectors of its two sides. Questions ask, "Why is PA = PC? Why is PB = PC? Deduce that PA = PB."
In such a manner, the student is gently led to deduce the statement: The perpendicular bisectors of the sides of any triangle all meet in a single point.
You can see all this for yourself in these two sample pages:
The chapters in the book
-
The Shortest Path. The "central" or opening problem for this chapter presents a camper in a forest who needs to return to his campsite, but first he needs to fetch a bucket of water from the river. The problem is, "At what point P on the river should he fill his pail in order to make the shortest possible path to put out the fire?"
This single problem leads to the development of several important concepts: distance from a point to a line, perpendicular lines, and reflection of a point across a line. Students then study the exact solution and its proof, along with applications.
Below you can preview the pages 6-9 of the first chapter, which show the development of concepts (such as reflections and triangle inequality) towards the solution of the "shortest path" problem.




Tiling the Plane deals with polygons and angles, and of course solves the question as to which regular polygons tile the plane.
Triangles deals specifically with the SSS, SAS, and ASA congruence properties of triangles. This chapter also provides some practice in proving theorems.
What is a Proof? is about proofs and some common pitfalls in devising proofs. Along the way, the chapter also develops properties of quadrilaterals, especially of parallelograms.
Constructions with Straightedge and Compass covers basic constructions, the special points of a triangle, and also some impossible constructions.
Area and Volume is like the title suggests: areas and volumes of basic figures.
The Pythagorean Theorem
Similar Figures
Perimeter, Area, and Volume of Similar Figures
Circles – this chapter has an exceptional number of interesting projects.
Coordinates
Conic Sections – most of this chapter is devoted to the ellipse.
After the main worktext part (called Central) in each chapter, we find a Central Self Quiz, a review, a review self test, and projects, which contain the most interesting problems! There is also an algebra review at the end of chapters 1-7 and cumulative reviews at the end of chapters 3, 7, 9, and 12.
In the very end of each chapter you will find answers to the chapter's central self quiz, the review self test, algebra review, and most of the answers to the review.
The "projects" sections in the end of each chapter definitely have lots of interesting material. While they often deal with extensions of the main ideas of the chapter, you will also find explanations and explorations concerning mathematically important results, for example the golden section, geometric mean, additional proofs of the Pythagorean theorem, the number of diagonals in a convex polygon, regular polyhedra, Gauss' theorem concerning which regular polygons can be constructed, and the problem about squaring the circle.
In a regular classroom, these projects may get neglected or assigned only to the fastest students, but I would encourage you to really DELVE into them, as they often present the best and most fascinating parts of geometry -- all the while developing the student's reasoning skills.
How Geometry: A Guided Inquiry handles proof
Different geometry books handle the topic of proof in different manners, and teachers might prefer one approach over another, so I will now briefly describe how mathematical proof is approached in Geometry: A Guided Inquiry.
As explained above, this book often has a set of carefully crafted exercises leading to an important theorem, and these exercises build one upon another in a logical succession, either preparing the student to understand the proof of the particular theorem or to build one for it.
Starting in chapter 2 (Tiling the Plane), students are often asked to complete parts of an argument. In some exercises students are also asked to give an argument or explain his answers using a certain fact. I find these bird-size steps towards more formal proof to be very well designed.
In chapter 3, after studying the SSS, SAS, and ASA properties of triangles, we encounter the section Introduction to Proofs. In it, the student is again asked to fill in missing words or parts of sentences in paragraph-form proofs or supply reasons for a few two-column proofs. In other problems, the student is asked to write the proof first with a hint and later on without one.
The two pages below show an example of this.
Chapter 4 is titled, "What is a Proof?" It explains such basics as "If...then" statements, converses, and axioms, and lets students practice filling in proofs or writing their own in the context of properties of parallelograms. We also meet Alex and Danielle, who seem to manage to write flawed proofs all the time – so the reader can learn from their mistakes.
In the rest of the chapters, proofs are not forgotten; quite the contrary: the students are often asked to write them, often with a hint. On page 346 we find an example of circular reasoning. I also especially liked problems where you have to find what is wrong with each picture, when the pictures are purposefully drawn distorted. This practices simple logical reasoning not based on the appearance of the figure.
An axiomatic vs. discovery based geometry text
Geometry: A Guided Inquiry is NOT written in a strict formal axiomatic style à la Euclid. It does not start out by presenting a set of axioms in the very beginning and developing all theorems from those.
However, from chapter 2 on, it IS written as a system of geometry that is developed from axioms. This is just somewhat "hidden" from sight by the explorative exercises that precede the axioms and the theorems alike. Also, the few axioms are only introduced as they are needed. The emphasis is more on "local" proofs than on a "global" axiomatic system. Since the only difference between axiom and theorems is that the axioms are not proved, from a student's point of view both may just seem to be material or knowledge to be learned.
Personally I feel that the problem-solving approach of Geometry: A Guided Inquiry is first of all more student-friendly and "gentle" than a pure axiomatic text. Even more importantly, it truly focuses on the content of geometry rather than being merely a course on logic with a geometric backdrop. It DOES contain plenty of rigorous arguments, proofs, and practice in writing them, but it is all in a context of solving problems, blended in with the explorative and other kinds of exercises.
This, I feel, is a more natural way of learning material the first time around. Reading and following an axiomatically built mathematical work is easier once you have a good idea of the material it covers. Personally, I would additionally try to introduce students to Euclid's work and to the strictly axiomatic system just a little – not only for the sake of logic but also for its historical significance. Chandler's Home Study Companion (see below) contains some material to familiarize students with Euclid's work.
Research shows that students' geometrical understanding proceeds from reasoning about shapes based on their appearance gradually into logical and abstract reasoning. Studying high school geometry strictly as an axiomatic system is probably not the most productive way for the vast majority of students. (Please see the article Geometry and Proof by Michael T. Battista and Douglas H. Clements for more information.)
Home Study Companion By David Chandler
Home Study Companion: Geometry (HSC) by David Chandler really makes the textbook Geometry: A Guided Inquiry a home run for homeschoolers, because it provides complete, worked-out solutions (not just answers) to all the problems in the Central (the main worktext) and Project sections of the textbook. The book itself contains answers to its various review and self-test sections, yet Chandler includes complete solutions on video to all of the Review sections, which allow the student to see the complete problem solving process of the problems. With the Home Study Companion, you will always have help available should you get stuck while doing the problems or the projects from the textbook.
Not only that, but the Home Study Companion includes hundreds of interactive demonstrations using Geogebra, which is a free dynamic geometry software. These demonstrations cover most of the main concepts and many additional explorations of the Central and Projects sections of each chapter. Accompanying each demonstration (or cluster of demonstrations) is an activity guide (PDF file) that will help you get the most out of the Geogebra explorations and teach you how to use Geogebra as a tool on your own as well.
How do these demonstrations work? For example, let's say you're asked to prove that the diagonals of a parallelogram bisect each other. A Geogebra demonstration has a parallelogram and its diagonals, and shows you measurements of the two parts of each diagonal. You can then change the shape of the parallelogram in Geogebra (by dragging control points) and see that those measurements stay equal to each other. The interactive demo lets the student get a "hands-on" experience with the concept, thus helping the student understand the matter more deeply!
Here are some example screenshots. Click to enlarge. Keep in mind these screenshots are static, while the demonstrations are dynamic.
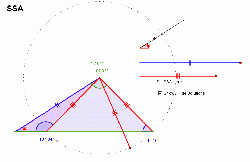 Attempting to speficy a triangle by SSA |
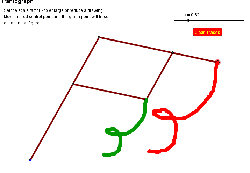 An interactive pantograph |
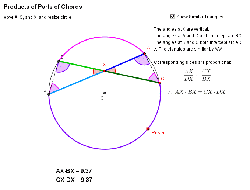 A theorem about the parts of intersecting chords in a circle |
|
Many of these demonstrations include animated demonstrations of theorems or even entire proofs (you tick boxes to reveal the steps). Each time, you can change the lengths, angles, or other features of the figure by dragging control points, and the demonstration still works. I was quite impressed!
For example, you can view several animated proofs of the Pythagorean theorem, how the angle sum of polygons truly works to be (n − 2)180°, how certain polygons tile the plane and others do not, and how Archimedes found an approximate value of Pi by approximating the area of a circle with polygons.
The interactive demonstrations add another dimension to the study of geometry by themselves, but your students can go even further: simply encourage them to learn Geogebra well enough to duplicate the demonstrations, including with color and animations. Computer-oriented children will love such challenge!
In addition to the demonstrations, the Home Study Companion also includes some additional lessons to supplement the main textbook. These extensions were originally added to bring the content of the text into alignment with California State Standards. The extensions included are: Isometries and Symmetry, More on Proof, Surface Areas of Prisms and Pyramids; Introduction to Trigonometry; Surface Areas of Cylinders, Cones, and Spheres; and More on Coordinate Geometry. Many of these topics are also found in the Common Core standards. They may or may not affect homeschoolers directly, but they are good supplementary topics.
Geogebra
Geogebra is a dynamic geometry software. This means that you can construct geometric objects by their relation to other objects, such as constructing a circle so that its center point is the point of intersection of certain line segments, and then you can "drag" the control points and observe the whole figure changing dynamically. Geogebra also has the capabilities for algebra, calculus, and statistics, and it is available in a multitude of languages.
You shouldn't restrict the usage of Geogebra for only viewing the demos in the Home Study Companion. Chandler explains the basics of how to use Geogebra in the activity guides, and your students can learn to do many constructions and exercises on their own. It's great fun — not unlike using construction toys, because you "build" objects/figures with the software and then check what changes when you move parts of it.
Geogebra also has a vibrant community of users that provide thousands of free worksheets and Geogebra books for you to download.
Conclusion
Overall, I feel this combo is very comprehensive, yet very suitable for a self-learning environment. You get a very logical and enjoyable textbook where exercises lead step-by-step to theorems or to proofs, solutions, interactive demonstrations, and a full-fledged geometry software to "play" with.
It is thus an excellent choice for doing high school geometry with a "guided inquiry" method. I especially applaud the very varied problems of the book and the quality of the demonstrations in the Home Study Companion.
One thing some people might find lacking is that the textbook won't work well as a reference book. You will not find all the main theorems on topic X clearly laid out in boxes with example pictures, followed by proofs. Instead, this is a "learn-by-doing" book. The important theorems and results are studied and proven in a very natural surrounding: while doing problems.
However, I would venture to say that this type of learning is longer-lasting than the traditional model of "theorem-proof-exercises".
Purchasing
- Home Study Companion is sold at Math Without Borders for $79 + shipping.
- Geogebra is free software.
- Geometry: A Guided Inquiry is out of print. However, you will get a free digital copy (PDF) when purchasing the Home Study Companion at Math Without Borders. :^)

The sample pages are images scanned from the book, reproduced here by permission from the publisher.
G.D. Chakerian, Crabill, Stein,
1998, Denver, CO: Morton Publishing Company (www.morton-pub.com).
Review by Maria Miller
Receive my monthly collection of math tips & resources directly in your inbox — and get a FREE Math Mammoth book!
You can unsubscribe at any time.
Math Mammoth TourConfused about the different options? Take a virtual email tour around Math Mammoth! You'll receive: An initial email to download your GIFT of over 400 free worksheets and sample pages from my books. Six other "TOURSTOP" emails that explain the important things and commonly asked questions concerning Math Mammoth curriculum. (Find out the differences between all these different-colored series!)This way, you'll have time to digest the information over one or two weeks, plus an opportunity to ask me personally about the curriculum. A monthly collection of math teaching tips & Math Mammoth updates (unsubscribe any time) We respect your email privacy.
Note: You will FIRST get an email that asks you to confirm your email address. If you cannot find this confirmation email, please check your SPAM/JUNK folder. |
"Mini" Math Teaching CourseThis is a little "virtual" 2-week course, where you will receive emails on important topics on teaching math, including:
- How to help a student who is behind You will also receive: A GIFT of over 400 free worksheets and sample pages from my books right in the very beginning.We respect your email privacy.
Note: You will FIRST get an email that asks you to confirm your email address. If you cannot find this confirmation email, please check your SPAM/JUNK folder. |
Maria's Math TipsEnter your email to receive math teaching tips, resources, Math Mammoth news & sales, humor, and more! I tend to send out these tips about once monthly, near the beginning of the month, but occasionally you may hear from me twice per month (and sometimes less often). Peek at the previous tips here. You will also receive:
We respect your email privacy.
|
|





